Previous
 About HAP: Persistent Homology
 next

1. Persistent Homology of Cubical and Simplicial Complexes
An inclusion of pure cubical complexes X1 --> X2 induces a natural homology homomorphism Hn(X1,F) --> Hn(X2,F) for each positive n and any coefficient module F. Taking F to be a field, the induced homomorphism is a homomorphism of vector spaces and is completely determined by its rank P1,2.

A sequence of inclusions X1 --> X2 --> X3 --> ... --> Xk induces a sequence of homology homomorphisms which, in each degree n, determine a kxk matrix of ranks Pi,j  (where for i>j we define Pi,j=0). This matrix is referred to as the n-th persistence matrix, over the field F, for the sequence of pure cubical complexes.

A possible scenario is that X1 is a sample from an unknown manifold M, and that each space Xi+1 is obtained by thickening Xi in some fashion. The hope is that the persistence matrices describe the shape of the manifold M from which X1 was sampled. 
Persistence matrices are particularly useful when analysing high-dimensional data since the shape of such data is hard to visualize. However, as a toy example let us consider the 2-dimensional data cloud



which, as we can see, was sampled (possibly with error) from an annulus. The following computations agree with this observation.

The following commands produce a sequence of thickenings for this data cloud and then compute the degree 1 persistence matrix over the field of rational numbers.
gap> M:=ReadImageAsPureCubicalComplex("datacloud.eps",300);
Pure cubical complex of dimension 2.

gap> T:=ThickeningFiltration(M,10);                       
Filtered pure cubical complex of dimension 2.

gap> P:=PersistentHomologyOfFilteredCubicalComplex(T,1);;
The persistence matrix P can be viewed as a barcode. The following command displays this barcode. The single horizontal line at the bottom of the barcode corresponds to a single persistent 1-dimensional homology. This is consistent with the data having been sampled from an annulus - a space with a single 1-dimensional hole. The various dots in the barcode correspond to homologies that arise briefly at various stages in the thickening process.
gap> BarCodeDisplay(P);
As a more realistic illustration of this approach to topological data analysis let us suppose that we have made 400 experimental observations v1, ..., v400 and that we are able to estimate some metric distance d(vi,vj) between each pair of observations. For instance, the observations might be vectors of a given length and  d(vi,vj) could be the Euclidean distance. We could then build a filtered simplicial complex K={K1<K2<...<KT} from an increasing sequence of thresholds d1<...<dT. Each term in the filtration has 400 vertices v1, ..., v400, and  Kt is determined by the threshold dt: a simplex belongs to Kt is and only if each pair of vertices in the simplex satisfies d(vi,vj) < dt . The persistent homology of the filtered simplicial complex K could provide information on the space from which our data was selected.

The following data

v1
 v2
   ...
 v399
 v400
v1
 0
 66
191
 137
v2
 66
 0
125
 71
...




v399
 191
 125
0
 54
v400
 137
 71
54
 0
 
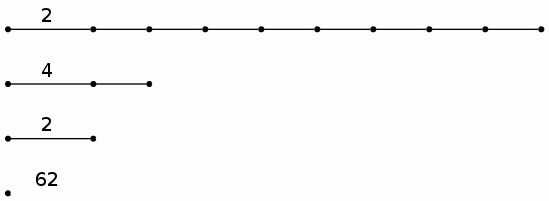
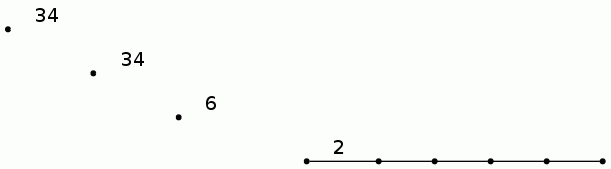
is contained in a symmetric matrix in the file symmetricMatrix.txt . The following commands read this matrix, compute the filtered simplicial complex, and then compute the barcodes for 0-dimensional and 1-dimensional homology. These barcodes suggest that the data points were samples from a space with the homology of a disjoint union of two circles.

We view the barcodes in compact form, where a line with label n is used to denote n lines which start at the same point in the filtration and end at the same point in the filtration.
gap> Read("symmetricMatrix.txt");
gap> S:=SymmetricMat;;
gap> G:=SymmetricMatrixToFilteredGraph(S,10,30);; #Take a filtration with length T=10, and discard any distances greater than 30.
gap> N:=SimplicialNerveOfFilteredGraph(G,2);;
gap> C:=SparseFilteredChainComplexOfFilteredSimplicialComplex(N);;
gap> P0:=PersistentHomologyOfFilteredSparseChainComplex(C,0);;
gap> P1:=PersistentHomologyOfFilteredSparseChainComplex(C,1);;

gap> BarCodeCompactDisplay(P0);



gap>BarCodeCompactDisplay(P1);
A different scenario for the use of persitent homology of pure cubical complexes is in the analysis of digital images. As a second toy example consider the digital photo.



The 20 longish lines in the following barcode for the degree 0 persistent homology correspond to the 20 objects in the photo. The 14 longish lines in the following barcode for the degree 1 persistent homology correspond to the fact that 14 of the objects have holes in them. We again view the barcodes in compact form, where a line with label n is used to denote n lines which start at the same point in the filtration and end at the same point in the filtration.
gap> F:=ReadImageAsFilteredCubicalComplex("image1.3.2.png",20);
Filtered pure cubical complex of dimension 2.

gap> P0:=PersistentHomologyOfFilteredCubicalComplex(F,0);;
gap> BarCodeCompactDisplay(P0);



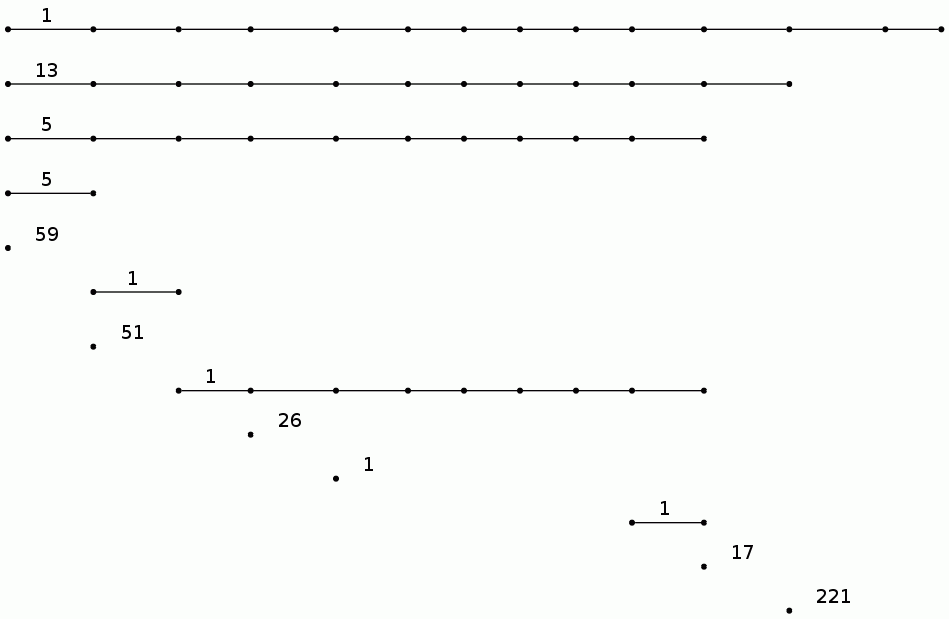
gap> P1:=PersistentHomologyOfFilteredCubicalComplex(F,1);;
gap> BarCodeCompactDisplay(P1);
2. Persistent Homology of Proteins
Given a pure cubical complex K, let us denote its centre of gravity by c(K). Given an increasing sequence of positive numbers 0 < t1  < t2 < ... ,   let us denote by FKn the intersection of K with the Euclidean ball of radius tn centred at c(K). This gives rise to a filtered pure cubical complex FK1 < FK2 < ... which we refer to as the concetric filtration on K.

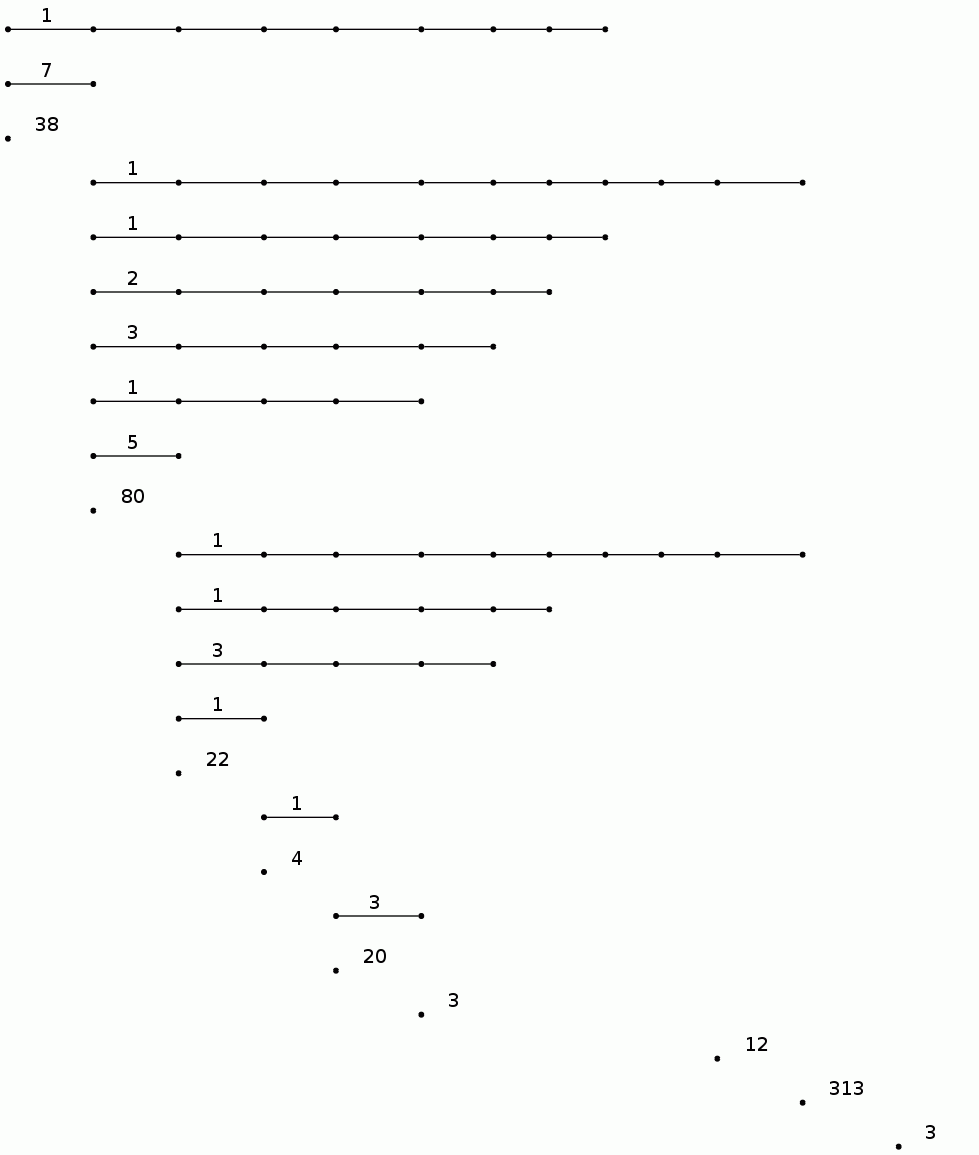
For a protein backbone K, the degree 0 persistent homology of FK should contain useful information on the geometric shape of K.

The following commands compute this shape descriptor for the T.thermophilus 1V2X protein and the H.sapiens 1XD3 protein pictured on the previous page.
gap> K:=ReadPDBfileAsPureCubicalComplex("1V2X.pdb");;      
Reading chain containing 191 atoms.
gap> FK:=ConcentricallyFilteredPureCubicalComplex(K,10);;
gap> P:=PersistentHomologyOfFilteredCubicalComplex(FK,0);;
gap> BarCodeCompactDisplay(P);




gap> K:=ReadPDBfileAsPureCubicalComplex("1XD3.pdb");;    
Reading chain containing 243 atoms.
gap> FK:=ConcentricallyFilteredPureCubicalComplex(K,10);;
gap> P:=PersistentHomologyOfFilteredCubicalComplex(FK,0);;
gap> BarCodeCompactDisplay(P);
3. Persistent Homology of Groups
Any sequence of group homomorphisms G1 --> G2 --> ... --> Gk induces a sequence of homology homomorphisms. In particular, the successive quotients of a group G by the terms of its upper central series give a sequence of group homomorphisms that induces an interesting sequence of homology homomorphisms.

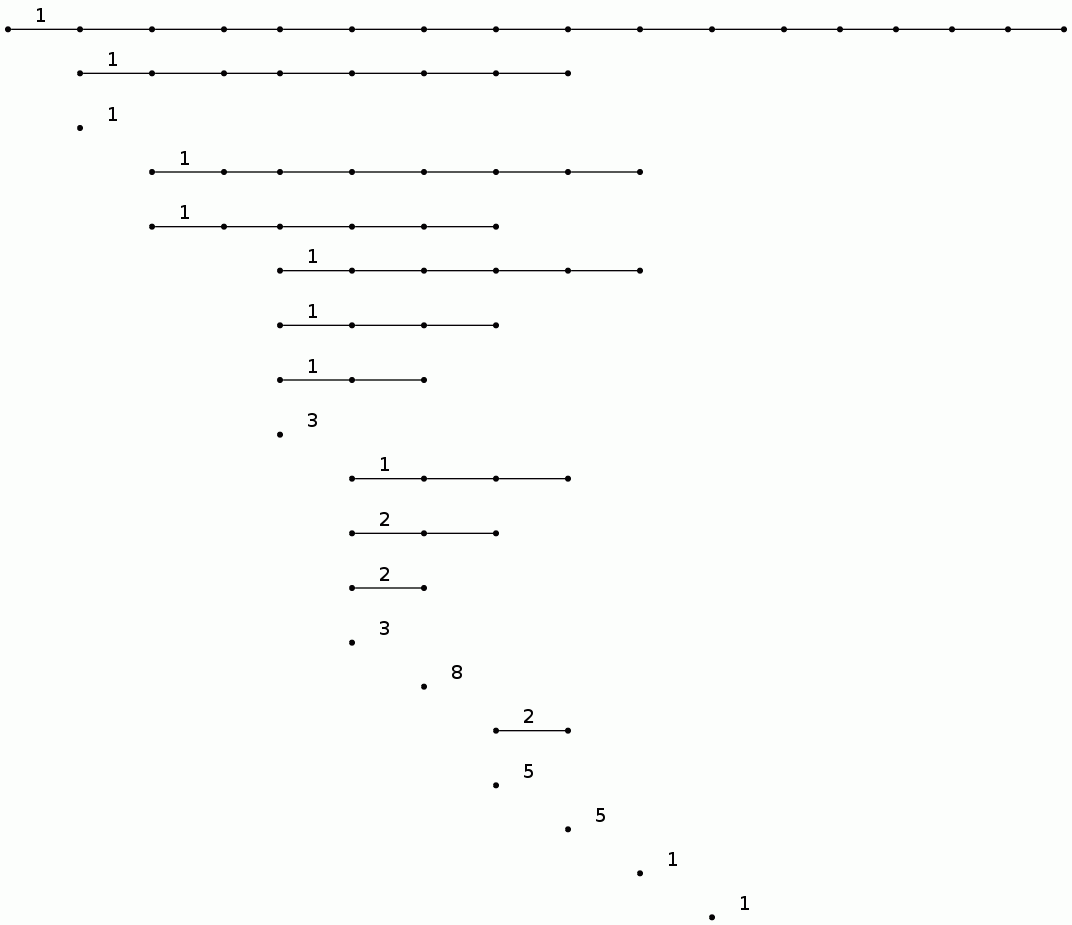
For a finite p-group we take homology coefficients in the field of p elements. The following commands compute and display the degree 3 homology barcode for the Sylow 2-subgroup of the Mathieu group M12.
gap> G:=SylowSubgroup(MathieuGroup(12),2);;

gap> IdGroup(G);
[ 64, 134 ]

gap> P:=UniversalBarCode("UpperCentralSeries",64,134,3);;

gap> BarCodeDisplay(P);
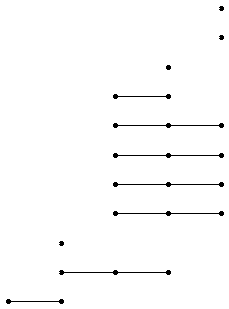
4. Persistent Homology of Filtered Chain Complexes
The Lyndon-Hochschild-Serre spectral sequence in group homology describes the homology of a group G in terms of the homology of a normal subgroup N and the homology of the quotient G/N. The spectral sequence arises from a filtered chain complex. Barcodes can be used to represent the differentials in this spectral sequence.

For example, the following commands produce the degree 2 mod 2 homology LHS barcode for G the diherdal group of order 64 and N its centre.
gap> G:=DihedralGroup(64);;
gap> N:=Center(G);;
gap> R:=ResolutionNormalSeries([G,N],3);;
gap> C:=FilteredTensorWithIntegersModP(R,2);;
gap> P:=PersistentHomologyOfFilteredChainComplex(C,2,2);;
gap> BarCodeDisplay(P);
Previous Page
 Contents
 Next page