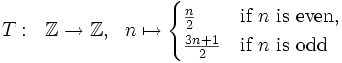
This package permits to compute in monoids, in particular groups, whose elements are residue-class-wise affine mappings. Probably the widest-known occurrence of such a mapping is in the statement of the 3n+1 conjecture, which asserts that iterated application of the Collatz mapping
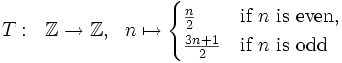
to any given positive integer eventually yields 1 (cf. [Lag03]). For definitions, see Section 2.1.
Presently, most research in computational group theory focuses on finite permutation groups, matrix groups, finitely presented groups, polycyclically presented groups and automata groups. For details, we refer to [HEO05]. The purpose of this package is twofold:
On the one hand, it provides the means to deal with another large class of groups which are accessible to computational methods, and it therefore extends the range of groups which can be dealt with by means of computation.
On the other -- and perhaps more importantly -- residue-class-wise affine groups appear to be interesting mathematical objects in their own right, and this package is intended to serve as a tool to obtain a better understanding of their rich and often complicated group theoretical and combinatorial structure.
In principle this package permits to construct and investigate all groups which have faithful representations as residue-class-wise affine groups. Among many others, the following groups and their subgroups belong to this class:
Finite groups, and certain divisible torsion groups which they embed into.
Free groups of finite rank.
Free products of finitely many finite groups.
Direct products of the above groups.
Wreath products of the above groups with finite groups and with (ℤ,+).
This list permits already to conclude that there are finitely generated residue-class-wise affine groups which do not have finite presentations, and such with algorithmically unsolvable membership problem. However the list is certainly by far not exhaustive, and using this package it is easy to construct groups of types which are not mentioned there.
The group CT(ℤ) which is generated by all class transpositions of ℤ -- these are involutions which interchange two disjoint residue classes, see ClassTransposition (2.2-3) -- is a simple group which has subgroups of all types listed above. It is countable, but it has an uncountable series of simple subgroups which is parametrized by the sets of odd primes.
Proofs of most of the results mentioned so far can be found in [Koh10]. Descriptions of a part of the algorithms and methods which are implemented in this package can be found in [Koh08].
The reader might want to know what type of results one can obtain with RCWA. However, the answer to this is that the package can be applied in various ways to various different problems, and it is simply not possible to say in general what can be found out with its help. So one really cannot give a better answer here than for the same question about GAP itself. The best way to get familiar with the package and its capabilities is likely to experiment with the examples discussed in this manual and the groups generated by 3 class transpositions from the corresponding data library.
Of course, sometimes this package does not provide an out-of-the-box solution for a given problem. But quite often it is still possible to find an answer by an interactive trial-and-error approach. With substantial help of this package, the author has found the results mentioned above. Interactive sessions with this package have also led to the development of most of the algorithms which are now implemented in it. Just to mention one example, developing the factorization method for residue-class-wise affine permutations (see FactorizationIntoCSCRCT (2.5-2)) solely by means of theory would likely have been very hard.
generated by GAPDoc2HTML