[MathJax off] [Style]

13 Congruence Subgroups, Cuspidal Cohomology and Hecke Operators

In this chapter we explain how HAP can be used to make computions about modular forms associated to congruence subgroups $\Gamma$ of $SL_2(\mathbb Z)$. Also, in Subsection 10.8 onwards, we demonstrate cohomology computations for the Picard group $SL_2(\mathbb Z[i])$, some Bianchi groups $PSL_2({\cal O}_{-d})$ where ${\cal O}_{d}$ is the ring of integers of $\mathbb Q(\sqrt{-d})$ for square free positive integer $d$, and some other groups of the form $SL_m({\cal O})$, $GL_m({\cal O})$, $PSL_m({\cal O})$, $PGL_m({\cal O})$, for $m=2,3,4$ and certain ${\cal O}=\mathbb Z, {\cal O}_{-d}$.

13.1 Eichler-Shimura isomorphism

We begin by recalling the Eichler-Shimura isomorphism [Eic57][Shi59]

$$S_k(\Gamma) \oplus \overline{S_k(\Gamma)} \oplus E_k(\Gamma) \cong_{\sf Hecke} H^1(\Gamma,P_{\mathbb C}(k-2))$$

which relates the cohomology of groups to the theory of modular forms associated to a finite index subgroup $\Gamma$ of $SL_2(\mathbb Z)$. In subsequent sections we explain how to compute with the right-hand side of the isomorphism. But first, for completeness, let us define the terms on the left-hand side.

Let $N$ be a positive integer. A subgroup $\Gamma$ of $SL_2(\mathbb Z)$ is said to be a congruence subgroup of level $N$ if it contains the kernel of the canonical homomorphism $\pi_N\colon SL_2(\mathbb Z) \rightarrow SL_2(\mathbb Z/N\mathbb Z)$. So any congruence subgroup is of finite index in $SL_2(\mathbb Z)$, but the converse is not true.

One congruence subgroup of particular interest is the group $\Gamma_1(N)=\ker(\pi_N)$, known as the principal congruence subgroup of level $N$. Another congruence subgroup of particular interest is the group $\Gamma_0(N)$ of those matrices that project to upper triangular matrices in $SL_2(\mathbb Z/N\mathbb Z)$.

A modular form of weight $k$ for a congruence subgroup $\Gamma$ is a complex valued function on the upper-half plane, $f\colon {\frak{h}}=\{z\in \mathbb C : Re(z)>0\} \rightarrow \mathbb C$, satisfying:

• $\displaystyle f(\frac{az+b}{cz+d}) = (cz+d)^k f(z)$ for $\left(\begin{array}{ll}a&b\\ c &d \end{array}\right) \in \Gamma$,

• $f$ is `holomorphic' on the extended upper-half plane $\frak{h}^\ast = \frak{h} \cup \mathbb Q \cup \{\infty\}$ obtained from the upper-half plane by `adjoining a point at each cusp'.

The collection of all weight $k$ modular forms for $\Gamma$ form a vector space $M_k(\Gamma)$ over $\mathbb C$.

A modular form $f$ is said to be a cusp form if $f(\infty)=0$. The collection of all weight $k$ cusp forms for $\Gamma$ form a vector subspace $S_k(\Gamma)$. There is a decomposition

$$M_k(\Gamma) \cong S_k(\Gamma) \oplus E_k(\Gamma)$$

involving a summand $E_k(\Gamma)$ known as the Eisenstein space. See [Ste07] for further introductory details on modular forms.

The Eichler-Shimura isomorphism is more than an isomorphism of vector spaces. It is an isomorphism of Hecke modules: both sides admit notions of Hecke operators, and the isomorphism preserves these operators. The bar on the left-hand side of the isomorphism denotes complex conjugation, or anti-holomorphic forms. See [Wie78] for a full account of the isomorphism.

On the right-hand side of the isomorphism, the $\mathbb Z\Gamma$-module $P_{\mathbb C}(k-2)\subset \mathbb C[x,y]$ denotes the space of homogeneous degree $k-2$ polynomials with action of $\Gamma$ given by

$$\left(\begin{array}{ll}a&b\\ c &d \end{array}\right)\cdot p(x,y) = p(dx-by,-cx+ay)\ .$$

In particular $P_{\mathbb C}(0)=\mathbb C$ is the trivial module. Below we shall compute with the integral analogue $P_{\mathbb Z}(k-2) \subset \mathbb Z[x,y]$.

In the following sections we explain how to use the right-hand side of the Eichler-Shimura isomorphism to compute eigenvalues of the Hecke operators restricted to the subspace $S_k(\Gamma)$ of cusp forms.

13.2 Generators for $SL_2(\mathbb Z)$ and the cubic tree

The matrices $S=\left(\begin{array}{rr}0&-1\\ 1 &0 \end{array}\right)$ and $T=\left(\begin{array}{rr}1&1\\ 0 &1 \end{array}\right)$ generate $SL_2(\mathbb Z)$ and it is not difficult to devise an algorithm for expressing an arbitrary integer matrix $A$ of determinant $1$ as a word in $S$, $T$ and their inverses. The following illustrates such an algorithm.

gap> A:=[[4,9],[7,16]];;
gap> word:=AsWordInSL2Z(A);
[ [ [ 1, 0 ], [ 0, 1 ] ], [ [ 0, 1 ], [ -1, 0 ] ], [ [ 1, -1 ], [ 0, 1 ] ], 
  [ [ 0, 1 ], [ -1, 0 ] ], [ [ 1, 1 ], [ 0, 1 ] ], [ [ 0, 1 ], [ -1, 0 ] ], 
  [ [ 1, -1 ], [ 0, 1 ] ], [ [ 1, -1 ], [ 0, 1 ] ], [ [ 1, -1 ], [ 0, 1 ] ], 
  [ [ 0, 1 ], [ -1, 0 ] ], [ [ 1, 1 ], [ 0, 1 ] ], [ [ 1, 1 ], [ 0, 1 ] ] ]
gap> Product(word);
[ [ 4, 9 ], [ 7, 16 ] ]

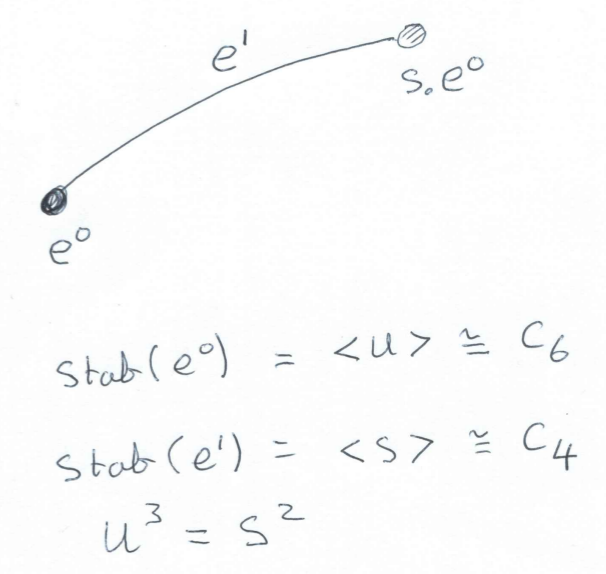
It is convenient to introduce the matrix $U=ST = \left(\begin{array}{rr}0&-1\\ 1 &1 \end{array}\right)$. The matrices $S$ and $U$ also generate $SL_2(\mathbb Z)$. In fact we have a free presentation $SL_2(\mathbb Z)= \langle S,U\, |\, S^4=U^6=1, S^2=U^3 \rangle$.

The cubic tree $\cal T$ is a tree (i.e. a $1$-dimensional contractible regular CW-complex) with countably infinitely many edges in which each vertex has degree $3$. We can realize the cubic tree $\cal T$ by taking the left cosets of ${\cal U}=\langle U\rangle$ in $SL_2(\mathbb Z)$ as vertices, and joining cosets $x\,{\cal U}$ and $y\,{\cal U}$ by an edge if, and only if, $x^{-1}y \in {\cal U}\, S\,{\cal U}$. Thus the vertex $\cal U$ is joined to $S\,{\cal U}$, $US\,{\cal U}$ and $U^2S\,{\cal U}$. The vertices of this tree are in one-to-one correspondence with all reduced words in $S$, $U$ and $U^2$ that, apart from the identity, end in $S$.

From our realization of the cubic tree $\cal T$ we see that $SL_2(\mathbb Z)$ acts on $\cal T$ in such a way that each vertex is stabilized by a cyclic subgroup conjugate to ${\cal U}=\langle U\rangle$ and each edge is stabilized by a cyclic subgroup conjugate to ${\cal S} =\langle S \rangle$.

In order to store this action of $SL_2(\mathbb Z)$ on the cubic tree $\cal T$ we just need to record the following finite amount of information.

13.3 One-dimensional fundamental domains and generators for congruence subgroups

The modular group ${\cal M}=PSL_2(\mathbb Z)$ is isomorphic, as an abstract group, to the free product $\mathbb Z_2\ast \mathbb Z_3$. By the Kurosh subgroup theorem, any finite index subgroup $M \subset {\cal M}$ is isomorphic to the free product of finitely many copies of $\mathbb Z_2$s, $\mathbb Z_3$s and $\mathbb Z$s. A subset $\underline x \subset M$ is an independent set of subgroup generators if $M$ is the free product of the cyclic subgroups $<x >$ as $x$ runs over $\underline x$. Let us say that a set of elements in $SL_2(\mathbb Z)$ is projectively independent if it maps injectively onto an independent set of subgroup generators $\underline x\subset {\cal M}$. The generating set $\{S,U\}$ for $SL_2(\mathbb Z)$ given in the preceding section is projectively independent.

We are interested in constructing a set of generators for a given congruence subgroup $\Gamma$. If a small generating set for $\Gamma$ is required then we should aim to construct one which is close to being projectively independent.

It is useful to invoke the following general result which follows from a perturbation result about free $\mathbb ZG$-resolutons in [EHS06, Theorem 2] and an old observation of John Milnor that a free $\mathbb ZG$-resolution can be realized as the cellular chain complex of a CW-complex if it can be so realized in low dimensions.

Theorem. Let $X$ be a contractible CW-complex on which a group $G$ acts by permuting cells. The cellular chain complex $C_\ast X$ is a $\mathbb ZG$-resolution of $\mathbb Z$ which typically is not free. Let $[e^n]$ denote the orbit of the n-cell $e^n$ under the action. Let $G^{e^n} \le G$ denote the stabilizer subgroup of $e^n$, in which group elements are not required to stabilize $e^n$ point-wise. Let $Y_{e^n}$ denote a contractible CW-complex on which $G^{e^n}$ acts cellularly and freely. Then there exists a contractible CW-complex $W$ on which $G$ acts cellularly and freely, and in which the orbits of $n$-cells are labelled by $[e^p]\otimes [f^q]$ where $p+q=n$ and $[e^p]$ ranges over the $G$-orbits of $p$-cells in $X$, $[f^q]$ ranges over the $G^{e^p}$-orbits of $q$-cells in $Y_{e^p}$.

Let $W$ be as in the theorem. Then the quotient CW-complex $B_G=W/G$ is a classifying space for $G$. Let $T$ denote a maximal tree in the $1$-skeleton $B^1_G$. Basic geometric group theory tells us that the $1$-cells in $B^1_G\setminus T$ correspond to a generating set for $G$.

Suppose we wish to compute a set of generators for a principal congruence subgroup $\Gamma=\Gamma_1(N)$. In the above theorem take $X={\cal T}$ to be the cubic tree, and note that $\Gamma$ acts freely on $\cal T$ and thus that $W={\cal T}$. To determine the $1$-cells of $B_{\Gamma}\setminus T$ we need to determine a cellular subspace $D_\Gamma \subset \cal T$ whose images under the action of $\Gamma$ cover $\cal T$ and are pairwise either disjoint or identical. The subspace $D_\Gamma$ will not be a CW-complex as it won't be closed, but it can be chosen to be connected, and hence contractible. We call $D_\Gamma$ a fundamental region for $\Gamma$. We denote by $\mathring D_\Gamma$ the largest CW-subcomplex of $D_\Gamma$. The vertices of $\mathring D_\Gamma$ are the same as the vertices of $D_\Gamma$. Thus $\mathring D_\Gamma$ is a subtree of the cubic tree with $|\Gamma|/6$ vertices. For each vertex $v$ in the tree $\mathring D_\Gamma$ define $\eta(v)=3 -{\rm degree}(v)$. Then the number of generators for $\Gamma$ will be $(1/2)\sum_{v\in \mathring D_\Gamma} \eta(v)$.

The following commands determine projectively independent generators for $\Gamma_1(6)$ and display $\mathring D_{\Gamma_1(6)}$. The subgroup $\Gamma_1(6)$ is free on $13$ generators.

gap> G:=HAP_PrincipalCongruenceSubgroup(6);;
gap> HAP_SL2TreeDisplay(G);


gap> gens:=GeneratorsOfGroup(G);
[ [ [ -83, -18 ], [ 60, 13 ] ], [ [ -77, -18 ], [ 30, 7 ] ], 
  [ [ -65, -12 ], [ 168, 31 ] ], [ [ -53, -12 ], [ 84, 19 ] ], 
  [ [ -47, -18 ], [ 222, 85 ] ], [ [ -41, -12 ], [ 24, 7 ] ], 
  [ [ -35, -6 ], [ 6, 1 ] ], [ [ -11, -18 ], [ 30, 49 ] ], 
  [ [ -11, -6 ], [ 24, 13 ] ], [ [ -5, -18 ], [ 12, 43 ] ], 
  [ [ -5, -12 ], [ 18, 43 ] ], [ [ -5, -6 ], [ 6, 7 ] ], 
  [ [ 1, 0 ], [ -6, 1 ] ] ]

An alternative but very related approach to computing generators of congruence subgroups of $SL_2(\mathbb Z)$ is described in [Kul91].

The congruence subgroup $\Gamma_0(N)$ does not act freely on the vertices of $\cal T$, and so one needs to incorporate a generator for the cyclic stabilizer group according to the above theorem. Alternatively, we can replace the cubic tree by a six-fold cover ${\cal T}'$ on whose vertex set $\Gamma_0(N)$ acts freely. This alternative approach will produce a redundant set of generators. The following commands display $\mathring D_{\Gamma_0(39)}$ for a fundamental region in ${\cal T}'$. They also use the corresponding generating set for $\Gamma_0(39)$, involving $18$ generators, to compute the abelianization $\Gamma_0(39)^{ab}= \mathbb Z_2 \oplus \mathbb Z_3^2 \oplus \mathbb Z^9$. The abelianization shows that any generating set has at least $11$ generators.

gap> G:=HAP_CongruenceSubgroupGamma0(39);;
gap> HAP_SL2TreeDisplay(G);
gap> Length(GeneratorsOfGroup(G));
18
gap> AbelianInvariants(G);
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 3, 3 ]

Note that to compute $D_\Gamma$ one only needs to be able to test whether a given matrix lies in $\Gamma$ or not. Given an inclusion $\Gamma'\subset \Gamma$ of congruence subgroups, it is straightforward to use the trees $\mathring D_{\Gamma'}$ and $\mathring D_{\Gamma}$ to compute a system of coset representative for $\Gamma'\setminus \Gamma$.

13.4 Cohomology of congruence subgroups

To compute the cohomology $H^n(\Gamma,A)$ of a congruence subgroup $\Gamma$ with coefficients in a $\mathbb Z\Gamma$-module $A$ we need to construct $n+1$ terms of a free $\mathbb Z\Gamma$-resolution of $\mathbb Z$. We can do this by first using perturbation techniques (as described in [BE14]) to combine the cubic tree with resolutions for the cyclic groups of order $4$ and $6$ in order to produce a free $\mathbb ZG$-resolution $R_\ast$ for $G=SL_2(\mathbb Z)$. This resolution is also a free $\mathbb Z\Gamma$-resolution with each term of rank

$${\rm rank}_{\mathbb Z\Gamma} R_k = |G:\Gamma|\times {\rm rank}_{\mathbb ZG} R_k\ .$$

For congruence subgroups of lowish index in $G$ this resolution suffices to make computations.

The following commands compute

$$H^1(\Gamma_0(39),\mathbb Z) = \mathbb Z^9\ .$$

gap> R:=ResolutionSL2Z_alt(2);
Resolution of length 2 in characteristic 0 for SL(2,Integers) .

gap> gamma:=HAP_CongruenceSubgroupGamma0(39);;
gap> S:=ResolutionFiniteSubgroup(R,gamma);
Resolution of length 2 in characteristic 0 for 
CongruenceSubgroupGamma0( 39)  .

gap> Cohomology(HomToIntegers(S),1);
[ 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

This computation establishes that the space $M_2(\Gamma_0(39))$ of weight $2$ modular forms is of dimension $9$.

The following commands show that ${\rm rank}_{\mathbb Z\Gamma_0(39)} R_1 = 112$ but that it is possible to apply `Tietze like' simplifications to $R_\ast$ to obtain a free $\mathbb Z\Gamma_0(39)$-resolution $T_\ast$ with ${\rm rank}_{\mathbb Z\Gamma_0(39)} T_1 = 11$. It is more efficient to work with $T_\ast$ when making cohomology computations with coefficients in a module $A$ of large rank.

gap> S!.dimension(1);
112
gap> T:=TietzeReducedResolution(S);
Resolution of length 2 in characteristic 0 for CongruenceSubgroupGamma0(
39)  . 

gap> T!.dimension(1);
11

The following commands compute

$$H^1(\Gamma_0(39),P_{\mathbb Z}(8)) = \mathbb Z_3 \oplus \mathbb Z_6 \oplus \mathbb Z_{168} \oplus \mathbb Z^{84}\ ,$$

$$H^1(\Gamma_0(39),P_{\mathbb Z}(9)) = \mathbb Z_2 \oplus \mathbb Z_2 .$$

gap> P:=HomogeneousPolynomials(gamma,8);;
gap> c:=Cohomology(HomToIntegralModule(T,P),1);
[ 3, 6, 168, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
gap> Length(c);
87

gap> P:=HomogeneousPolynomials(gamma,9);;
gap> c:=Cohomology(HomToIntegralModule(T,P),1);
[ 2, 2 ]

This computation establishes that the space $M_{10}(\Gamma_0(39))$ of weight $10$ modular forms is of dimension $84$, and $M_{11}(\Gamma_0(39))$ is of dimension $0$. (There are never any modular forms of odd weight, and so $M_k(\Gamma)=0$ for all odd $k$ and any congruence subgroup $\Gamma$.)

13.4-1 Cohomology with rational coefficients

To calculate cohomology $H^n(\Gamma,A)$ with coefficients in a $\mathbb Q\Gamma$-module $A$ it suffices to construct a resolution of $\mathbb Z$ by non-free $\mathbb Z\Gamma$-modules where $\Gamma$ acts with finite stabilizer groups on each module in the resolution. Computing over $\mathbb Q$ is computationally less expensive than computing over $\mathbb Z$. The following commands first compute $H^1(\Gamma_0(39),\mathbb Q) = H_1(\Gamma_0(39),\mathbb Q)= \mathbb Q^9$. As a larger example, they then compute $H^1(\Gamma_0(2^{13}-1),\mathbb Q) =\mathbb Q^{1365}$ where $\Gamma_0(2^{13}-1)$ has index $8192$ in $SL_2(\mathbb Z)$.

gap> K:=ContractibleGcomplex("SL(2,Z)");
Non-free resolution in characteristic 0 for SL(2,Integers) . 

gap> gamma:=HAP_CongruenceSubgroupGamma0(39);;
gap> KK:=NonFreeResolutionFiniteSubgroup(K,gamma);
Non-free resolution in characteristic 0 for <matrix group with 
18 generators> . 

gap> C:=TensorWithRationals(KK);
gap> Homology(C,1);
9

gap> G:=HAP_CongruenceSubgroupGamma0(2^13-1);;
gap> IndexInSL2Z(G);
8192
gap> KK:=NonFreeResolutionFiniteSubgroup(K,G);;
gap> C:=TensorWithRationals(KK);;
gap> Homology(C,1);
1365

13.5 Cuspidal cohomology

To define and compute cuspidal cohomology we consider the action of $SL_2(\mathbb Z)$ on the upper-half plane ${\frak h}$ given by

$$\left(\begin{array}{ll}a&b\\ c &d \end{array}\right) z = \frac{az +b}{cz+d}\ .$$

A standard 'fundamental domain' for this action is the region

$$\begin{array}{ll} D=&\{z\in {\frak h}\ :\ |z| > 1, |{\rm Re}(z)| < \frac{1}{2}\} \\ & \cup\ \{z\in {\frak h} \ :\ |z| \ge 1, {\rm Re}(z)=-\frac{1}{2}\}\\ & \cup\ \{z \in {\frak h}\ :\ |z|=1, -\frac{1}{2} \le {\rm Re}(z) \le 0\} \end{array}$$

illustrated below.

The action factors through an action of $PSL_2(\mathbb Z) =SL_2(\mathbb Z)/\langle \left(\begin{array}{rr}-1&0\\ 0 &-1 \end{array}\right)\rangle$. The images of $D$ under the action of $PSL_2(\mathbb Z)$ cover the upper-half plane, and any two images have at most a single point in common. The possible common points are the bottom left-hand corner point which is stabilized by $\langle U\rangle$, and the bottom middle point which is stabilized by $\langle S\rangle$.

A congruence subgroup $\Gamma$ has a `fundamental domain' $D_\Gamma$ equal to a union of finitely many copies of $D$, one copy for each coset in $\Gamma\setminus SL_2(\mathbb Z)$. The quotient space $X=\Gamma\setminus {\frak h}$ is not compact, and can be compactified in several ways. We are interested in the Borel-Serre compactification. This is a space $X^{BS}$ for which there is an inclusion $X\hookrightarrow X^{BS}$ and this inclusion is a homotopy equivalence. One defines the boundary $\partial X^{BS} = X^{BS} - X$ and uses the inclusion $\partial X^{BS} \hookrightarrow X^{BS} \simeq X$ to define the cuspidal cohomology group, over the ground ring $\mathbb C$, as

$$H_{cusp}^n(\Gamma,P_{\mathbb C}(k-2)) = \ker (\ H^n(X,P_{\mathbb C}(k-2)) \rightarrow H^n(\partial X^{BS},P_{\mathbb C}(k-2)) \ ).$$

Strictly speaking, this is the definition of interior cohomology $H_!^n(\Gamma,P_{\mathbb C}(k-2))$ which in general contains the cuspidal cohomology as a subgroup. However, for congruence subgroups of $SL_2(\mathbb Z)$ there is equality $H_!^n(\Gamma,P_{\mathbb C}(k-2)) = H_{cusp}^n(\Gamma,P_{\mathbb C}(k-2))$.

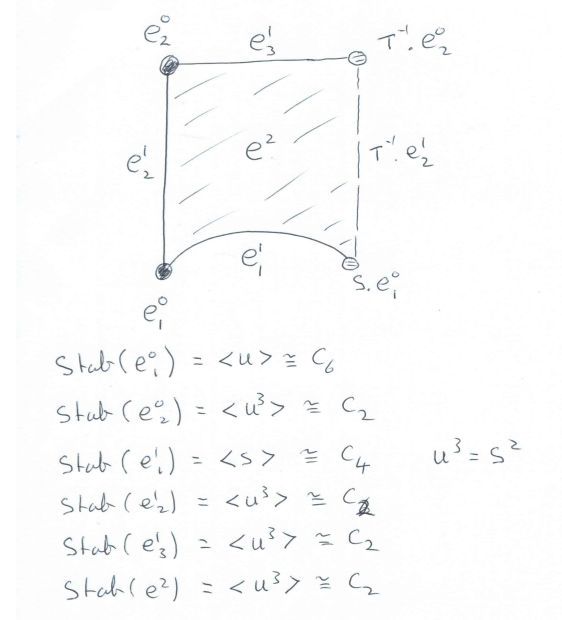
Working over $\mathbb C$ has the advantage of avoiding the technical issue that $\Gamma$ does not necessarily act freely on ${\frak h}$ since there are points with finite cyclic stabilizer groups in $SL_2(\mathbb Z)$. But it has the disadvantage of losing information about torsion in cohomology. So HAP confronts the issue by working with a contractible CW-complex $\tilde X^{BS}$ on which $\Gamma$ acts freely, and $\Gamma$-equivariant inclusion $\partial \tilde X^{BS} \hookrightarrow \tilde X^{BS}$. The definition of cuspidal cohomology that we use, which coincides with the above definition when working over $\mathbb C$, is

$$H_{cusp}^n(\Gamma,A) = \ker (\ H^n({\rm Hom}_{\, \mathbb Z\Gamma}(C_\ast(\tilde X^{BS}), A)\, ) \rightarrow H^n(\ {\rm Hom}_{\, \mathbb Z\Gamma}(C_\ast(\tilde \partial X^{BS}), A)\, \ ).$$

The following data is recorded and, using perturbation theory, is combined with free resolutions for $C_4$ and $C_6$ to constuct $\tilde X^{BS}$.

The following commands calculate

$$H^1_{cusp}(\Gamma_0(39),\mathbb Z) = \mathbb Z^6\ .$$

gap> gamma:=HAP_CongruenceSubgroupGamma0(39);;
gap> k:=2;; deg:=1;; c:=CuspidalCohomologyHomomorphism(gamma,deg,k);
[ g1, g2, g3, g4, g5, g6, g7, g8, g9 ] -> [ g1^-1*g3, g1^-1*g3, g1^-1*g3, 
  g1^-1*g3, g1^-1*g2, g1^-1*g3, g1^-1*g4, g1^-1*g4, g1^-1*g4 ]
gap> AbelianInvariants(Kernel(c));
[ 0, 0, 0, 0, 0, 0 ]

From the Eichler-Shimura isomorphism and the already calculated dimension of $M_2(\Gamma_0(39))\cong \mathbb C^9$, we deduce from this cuspidal cohomology that the space $S_2(\Gamma_0(39))$ of cuspidal weight $2$ forms is of dimension $3$, and the Eisenstein space $E_2(\Gamma_0(39))\cong \mathbb C^3$ is of dimension $3$.

The following commands show that the space $S_4(\Gamma_0(39))$ of cuspidal weight $4$ forms is of dimension $12$.

gap> gamma:=HAP_CongruenceSubgroupGamma0(39);;
gap> k:=4;; deg:=1;; c:=CuspidalCohomologyHomomorphism(gamma,deg,k);;
gap> AbelianInvariants(Kernel(c));
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]

13.6 Hecke operators on forms of weight 2

A congruence subgroup $\Gamma \le SL_2(\mathbb Z)$ and element $g\in SL_2(\mathbb Q)$ determine the subgroup $\Gamma' = \Gamma \cap g\Gamma g^{-1}$ and homomorphisms

$$\Gamma\ \hookleftarrow\ \Gamma'\ \ \stackrel{\gamma \mapsto g^{-1}\gamma g}{\longrightarrow}\ \ g^{-1}\Gamma' g\ \hookrightarrow \Gamma\ .$$

These homomorphisms give rise to homomorphisms of cohomology groups

$$H^n(\Gamma,\mathbb Z)\ \ \stackrel{tr}{\leftarrow} \ \ H^n(\Gamma',\mathbb Z) \ \ \stackrel{\alpha}{\leftarrow} \ \ H^n(g^{-1}\Gamma' g,\mathbb Z) \ \ \stackrel{\beta}{\leftarrow} H^n(\Gamma, \mathbb Z)$$

with $\alpha$, $\beta$ functorial maps, and $tr$ the transfer map. We define the composite $T_g=tr \circ \alpha \circ \beta\colon H^n(\Gamma, \mathbb Z) \rightarrow H^n(\Gamma, \mathbb Z)$ to be the Hecke operator determined by $g$. Further details on this description of Hecke operators can be found in [Ste07, Appendix by P. Gunnells].

For each prime integer $p\ge 1$ we set $T_p =T_g$ with for $g=\left(\begin{array}{cc}1&0\\0&p\end{array}\right)$.

The following commands compute $T_2$ and $T_5$ for $n=1$ and $\Gamma=\Gamma_0(39)$. The commands also compute the eigenvalues of these two Hecke operators. The final command confirms that $T_2$ and $T_5$ commute. (It is a fact that $T_pT_q=T_qT_p$ for all primes $p,q$.)

gap> gamma:=HAP_CongruenceSubgroupGamma0(39);;
gap> p:=2;;N:=1;;h:=HeckeOperatorWeight2(gamma,p,N);;
gap> AbelianInvariants(Source(h));
[ 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
gap> T2:=HomomorphismAsMatrix(h);;
gap> Display(T2);
[ [  -2,  -2,   2,   2,   1,   2,   0,   0,   0 ],
  [  -2,   0,   1,   2,  -2,   2,   2,   2,  -2 ],
  [  -2,  -1,   2,   2,  -1,   2,   1,   1,  -1 ],
  [  -2,  -1,   2,   2,   1,   1,   0,   0,   0 ],
  [  -1,   0,   0,   2,  -3,   2,   3,   3,  -3 ],
  [   0,   1,   1,   1,  -1,   0,   1,   1,  -1 ],
  [  -1,   1,   1,  -1,   0,   1,   2,  -1,   1 ],
  [  -1,  -1,   0,   2,  -3,   2,   1,   4,  -1 ],
  [   0,   1,   0,  -1,  -2,   1,   1,   1,   2 ] ]
gap> Eigenvalues(Rationals,T2);
[ 3, 1 ]

gap> p:=5;;N:=1;;h:=HeckeOperator(gamma,p,N);;
gap> T5:=HomomorphismAsMatrix(h);;
gap> Display(T5);
[ [  -1,  -1,   3,   4,   0,   0,   1,   1,  -1 ],
  [  -5,  -1,   5,   4,   0,   0,   3,   3,  -3 ],
  [  -2,   0,   4,   4,   1,   0,  -1,  -1,   1 ],
  [  -2,   0,   3,   2,  -3,   2,   4,   4,  -4 ],
  [  -4,  -2,   4,   4,   3,   0,   1,   1,  -1 ],
  [  -6,  -4,   5,   6,   1,   2,   2,   2,  -2 ],
  [   1,   5,   0,  -4,  -3,   2,   5,  -1,   1 ],
  [  -2,  -2,   2,   4,   0,   0,  -2,   4,   2 ],
  [   1,   3,   0,  -4,  -4,   2,   2,   2,   4 ] ]
gap> Eigenvalues(Rationals,T5);
[ 6, 2 ]

gap>T2*T5=T5*T2;
true

13.7 Hecke operators on forms of weight $\ge 2$

The above definition of Hecke operator $T_g$ for $g\in SL_2(\mathbb Q)$ extends to a Hecke operator $T_g\colon H^1(\Gamma,P_{\mathbb Q}(k-2) ) \rightarrow H^1(\Gamma,P_{\mathbb Q}(k-2) )$ for $k\ge 2$. We work over the rationals rather than the integers in order to ensure that the action of $\Gamma$ on homogeneous polynomials extends to an action of $g$. The following commands compute the matrix of $T_2\colon H^1(\Gamma,P_{\mathbb Q}(k-2) ) \rightarrow H^1(\Gamma,P_{\mathbb Q}(k-2) )$ for $\Gamma=SL_2(\mathbb Z)$ and $k=4$;

gap> H:=HAP_CongruenceSubgroupGamma0(1);;
gap> h:=HeckeOperator(H,2,12);;Display(h);
[ [   2049,  -7560,      0 ],
  [      0,    -24,      0 ],
  [      0,      0,    -24 ] ]

13.8 Reconstructing modular forms from cohomology computations

Given a modular form $f\colon {\frak h} \rightarrow \mathbb C$ associated to a congruence subgroup $\Gamma$, and given a compact edge $e$ in the tessellation of ${\frak h}$ (i.e. an edge in the cubic tree $\cal T$) arising from the above fundamental domain for $SL_2(\mathbb Z)$, we can evaluate

$$\int_e f(z)\,dz \ .$$

In this way we obtain a cochain $f_1\colon C_1({\cal T}) \rightarrow \mathbb C$ in $Hom_{\mathbb Z\Gamma}(C_1({\cal T}), \mathbb C)$ representing a cohomology class $c(f) \in H^1(\, Hom_{\mathbb Z\Gamma}(C_\ast({\cal T}), \mathbb C) \,) = H^1(\Gamma,\mathbb C)$. The correspondence $f\mapsto c(f)$ underlies the Eichler-Shimura isomorphism. Hecke operators can be used to recover modular forms from cohomology classes.

Hecke operators restrict to operators on cuspidal cohomology. On the left-hand side of the Eichler-Shimura isomorphism Hecke operators restrict to operators $T_s\colon S_2(\Gamma) \rightarrow S_2(\Gamma)$ for $s\ge 1$.

Let us now introduce the function $q=q(z)=e^{2\pi i z}$ which is holomorphic on $\mathbb C$. For any modular form $f(z)$ there are numbers $a_s$ such that

$$f(z) = \sum_{s=0}^\infty a_sq^s$$

for all $z\in {\frak h}$. The form $f$ is a cusp form if $a_0=0$.

A non-zero cusp form $f\in S_2(\Gamma)$ is an eigenform if it is simultaneously an eigenvector for the Hecke operators $T_s$ for all $s =1,2,3,\cdots$. An eigenform is said to be normalized if its coefficient $a_1=1$. It turns out that if $f$ is a normalized eigenform then the coefficient $a_s$ is an eigenvalue for $T_s$ (see for instance [Ste07] for details). It can be shown [AL70] that $f\in S_2(\Gamma_0(N))$ admits a basis of eigenforms.

This all implies that, in principle, we can construct an approximation to an explicit basis for the space $S_2(\Gamma)$ of cusp forms by computing eigenvalues for Hecke operators.

Suppose that we would like a basis for $S_2(\Gamma_0(11))$. The following commands first show that $H^1_{cusp}(\Gamma_0(11),\mathbb Z)=\mathbb Z\oplus \mathbb Z$ from which we deduce that $S_2(\Gamma_0(11)) =\mathbb C$ is $1$-dimensional. Then eigenvalues of Hecke operators are calculated to establish that the modular form

$$f = q -2q^2 -q^3 +2q^4 +q^5 +2q^6 -2q^7 + -2q^9 -2q^{10} + \cdots$$

constitutes a basis for $S_2(\Gamma_0(11))$.

gap> gamma:=HAP_CongruenceSubgroupGamma0(11);;
gap> AbelianInvariants(Kernel(CuspidalCohomologyHomomorphism(gamma,1,2)));
[ 0, 0 ]

gap> T1:=HomomorphismAsMatrix(HeckeOperator(gamma,1,1));; Display(T1);
[ [  1,  0,  0 ],
  [  0,  1,  0 ],
  [  0,  0,  1 ] ]
gap> T2:=HomomorphismAsMatrix(HeckeOperator(gamma,2,1));; Display(T2);
[ [   3,  -4,   4 ],
  [   0,  -2,   0 ],
  [   0,   0,  -2 ] ]
gap> T3:=HomomorphismAsMatrix(HeckeOperator(gamma,3,1));; Display(T3);
[ [   4,  -4,   4 ],
  [   0,  -1,   0 ],
  [   0,   0,  -1 ] ]
gap> T5:=HomomorphismAsMatrix(HeckeOperator(gamma,5,1));; Display(T5);
[ [   6,  -4,   4 ],
  [   0,   1,   0 ],
  [   0,   0,   1 ] ]
gap> T7:=HomomorphismAsMatrix(HeckeOperator(gamma,7,1));; Display(T7);
[ [   8,  -8,   8 ],
  [   0,  -2,   0 ],
  [   0,   0,  -2 ] ]

For a normalized eigenform $f=1 + \sum_{s=2}^\infty a_sq^s$ the coefficients $a_s$ with $s$ a composite integer can be expressed in terms of the coefficients $a_p$ for prime $p$. If $r,s$ are coprime then $T_{rs} =T_rT_s$. If $p$ is a prime that is not a divisor of the level $N$ of $\Gamma$ then $a_{p^m} =a_{p^{m-1}}a_p - p a_{p^{m-2}}.$ If the prime $p$ divides $N$ then $a_{p^m} = (a_p)^m$. It thus suffices to compute the coefficients $a_p$ for prime integers $p$ only.

The following commands establish that $S_{12}(SL_2(\mathbb Z))$ has a basis consisting of one cusp eigenform

$q - 24q^2 + 252q^3 - 1472q^4 + 4830q^5 - 6048q^6 - 16744q^7 + 84480q^8 - 113643q^9$

$- 115920q^{10} + 534612q^{11} - 370944q^{12} - 577738q^{13} + 401856q^{14} + 1217160q^{15} + 987136q^{16}$

$- 6905934q^{17} + 2727432q^{18} + 10661420q^{19} + ...$

gap> H:=HAP_CongruenceSubgroupGamma0(1);;
gap> for p in [2,3,5,7,11,13,17,19] do
> T:=HeckeOperator(H,p,1,12);;
> Print("eigenvalues= ",Eigenvalues(Rationals,T), " and eigenvectors = ", Eigenvectors(Rationals,T)," for p= ",p,"\n");
> od;
eigenvalues= [ 2049, -24 ] and eigenvectors = [ [ 1, -2520/691, 0 ], [ 0, 1, 0 ], [ 0, 0, 1 ] ] for p= 2
eigenvalues= [ 177148, 252 ] and eigenvectors = [ [ 1, -2520/691, 0 ], [ 0, 1, 0 ], [ 0, 0, 1 ] ] for p= 3
eigenvalues= [ 48828126, 4830 ] and eigenvectors = [ [ 1, -2520/691, 0 ], [ 0, 1, 0 ], [ 0, 0, 1 ] ] for p= 5
eigenvalues= [ 1977326744, -16744 ] and eigenvectors = [ [ 1, -2520/691, 0 ], [ 0, 1, 0 ], [ 0, 0, 1 ] ] for p= 7
eigenvalues= [ 285311670612, 534612 ] and eigenvectors = [ [ 1, -2520/691, 0 ], [ 0, 1, 0 ], [ 0, 0, 1 ] ] for p= 11
eigenvalues= [ 1792160394038, -577738 ] and eigenvectors = [ [ 1, -2520/691, 0 ], [ 0, 1, 0 ], [ 0, 0, 1 ] ] for p= 13
eigenvalues= [ 34271896307634, -6905934 ] and eigenvectors = [ [ 1, -2520/691, 0 ], [ 0, 1, 0 ], [ 0, 0, 1 ] ] for p= 17
eigenvalues= [ 116490258898220, 10661420 ] and eigenvectors = [ [ 1, -2520/691, 0 ], [ 0, 1, 0 ], [ 0, 0, 1 ] ] for p= 19

13.9 The Picard group

Let us now consider the Picard group $G=SL_2(\mathbb Z[ i])$ and its action on upper-half space

$${\frak h}^3 =\{(z,t) \in \mathbb C\times \mathbb R\ |\ t > 0\} \ .$$

To describe the action we introduce the symbol $j$ satisfying $j^2=-1$, $ij=-ji$ and write $z+tj$ instead of $(z,t)$. The action is given by

$$\left(\begin{array}{ll}a&b\\ c &d \end{array}\right)\cdot (z+tj) \ = \ \left(a(z+tj)+b\right)\left(c(z+tj)+d\right)^{-1}\ .$$

Alternatively, and more explicitly, the action is given by

$$\left(\begin{array}{ll}a&b\\ c &d \end{array}\right)\cdot (z+tj) \ = \ \frac{(az+b)\overline{(cz+d) } + a\overline c t^2}{|cz +d|^2 + |c|^2t^2} \ +\ \frac{t}{|cz+d|^2+|c|^2t^2}\, j \ .$$

A standard 'fundamental domain' $D$ for this action is the following region (with some of the boundary points removed).

$$\{z+tj\in {\frak h}^3\ |\ 0 \le |{\rm Re}(z)| \le \frac{1}{2}, 0\le {\rm Im}(z) \le \frac{1}{2}, z\overline z +t^2 \ge 1\}$$

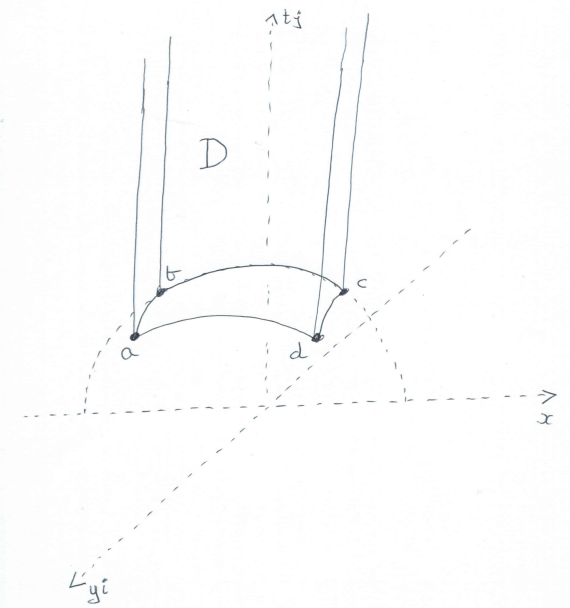
The four bottom vertices of $D$ are $a = -\frac{1}{2} +\frac{1}{2}i +\frac{\sqrt{2}}{2}j$, $b = -\frac{1}{2} +\frac{\sqrt{3}}{2}j$, $c = \frac{1}{2} +\frac{\sqrt{3}}{2}j$, $d = \frac{1}{2} +\frac{1}{2}i +\frac{\sqrt{2}}{2}j$.

The upper-half space ${\frak h}^3$ can be retracted onto a $2$-dimensional subspace ${\cal T} \subset {\frak h}^3$. The space ${\cal T}$ is a contractible $2$-dimensional regular CW-complex, and the action of the Picard group $G$ restricts to a cellular action of $G$ on ${\cal T}$.

Using perturbation techniques, the $2$-complex ${\cal T}$ can be combined with free resolutions for the cell stabilizer groups to contruct a regular CW-complex $X$ on which the Picard group $G$ acts freely. The following commands compute the first few terms of the free $\mathbb ZG$-resolution $R_\ast =C_\ast X$. Then $R_\ast$ is used to compute

$$H^1(G,\mathbb Z) =0\ ,$$

$$H^2(G,\mathbb Z) =\mathbb Z_2\oplus \mathbb Z_2\ ,$$

$$H^3(G,\mathbb Z) =\mathbb Z_6\ ,$$

$$H^4(G,\mathbb Z) =\mathbb Z_4\oplus \mathbb Z_{24}\ ,$$

and compute a free presentation for $G$ involving four generators and seven relators.

gap> K:=ContractibleGcomplex("SL(2,O-1)");;
gap> R:=FreeGResolution(K,5);;
gap> Cohomology(HomToIntegers(R),1);
[  ]
gap> Cohomology(HomToIntegers(R),2);
[ 2, 2 ]
gap> Cohomology(HomToIntegers(R),3);
[ 6 ]
gap> Cohomology(HomToIntegers(R),4);
[ 4, 24 ]
gap> P:=PresentationOfResolution(R);
rec( freeGroup := <free group on the generators [ f1, f2, f3, f4 ]>, 
  gens := [ 184, 185, 186, 187 ], 
  relators := [ f1^2*f2^-1*f1^-1*f2^-1, f1*f2*f1*f2^-2, 
      f3*f2^2*f1*(f2*f1^-1)^2*f3^-1*f1^2*f2^-2, 
      f1*(f2*f1^-1)^2*f3^-1*f1^2*f2^-1*f3^-1, 
      f4*f2*f1*(f2*f1^-1)^2*f4^-1*f1*f2^-1, f1*f4^-1*f1^-2*f4^-1, 
      f3*f2*f1*(f2*f1^-1)^2*f4^-1*f1*f2^-1*f3^-1*f4*f2 ] )

We can also compute the cohomology of $G=SL_2(\mathbb Z[i])$ with coefficients in a module such as the module $P_{\mathbb Z[i]}(k)$ of degree $k$ homogeneous polynomials with coefficients in $\mathbb Z[i]$ and with the action described above. For instance, the following commands compute

$$H^1(G,P_{\mathbb Z[i]}(24)) = (\mathbb Z_2)^4 \oplus \mathbb Z_4 \oplus \mathbb Z_8 \oplus \mathbb Z_{40} \oplus \mathbb Z_{80}\, ,$$

$$H^2(G,P_{\mathbb Z[i]}(24)) = (\mathbb Z_2)^{24} \oplus \mathbb Z_{520030}\oplus \mathbb Z_{1040060} \oplus \mathbb Z^2\, ,$$

$$H^3(G,P_{\mathbb Z[i]}(24)) = (\mathbb Z_2)^{22} \oplus \mathbb Z_{4}\oplus (\mathbb Z_{12})^2 \, .$$

gap> G:=R!.group;;
gap> M:=HomogeneousPolynomials(G,24);;
gap> C:=HomToIntegralModule(R,M);;
gap> Cohomology(C,1);
[ 2, 2, 2, 2, 4, 8, 40, 80 ]
gap> Cohomology(C,2);
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 
  520030, 1040060, 0, 0 ]
gap> Cohomology(C,3);
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 4, 12, 12 
 ]

13.10 Bianchi groups

The Bianchi groups are the groups $G=PSL_2({\cal O}_{-d})$ where $d$ is a square free positive integer and ${\cal O}_{-d}$ is the ring of integers of the imaginary quadratic field $\mathbb Q(\sqrt{-d})$. More explicitly,

$${\cal O}_{-d} = \mathbb Z\left[\sqrt{-d}\right]~~~~~~~~ {\rm if~} d \equiv 1,2 {\rm ~mod~} 4\, ,$$

$${\cal O}_{-d} = \mathbb Z\left[\frac{1+\sqrt{-d}}{2}\right]~~~~~ {\rm if~} d \equiv 3 {\rm ~mod~} 4\, .$$

These groups act on upper-half space ${\frak h}^3$ in the same way as the Picard group. Upper-half space can be tessellated by a 'fundamental domain' for this action. Moreover, as with the Picard group, this tessellation contains a $2$-dimensional cellular subspace ${\cal T}\subset {\frak h}^3$ where ${\cal T}$ is a contractible CW-complex on which $G$ acts cellularly. It should be mentioned that the fundamental domain and the contractible $2$-complex ${\cal T}$ are not uniquely determined by $G$. Various algorithms exist for computing ${\cal T}$ and its cell stabilizers. One algorithm due to Swan [Swa71a] has been implemented by Alexander Rahm [Rah10] and the output for various values of $d$ are stored in HAP. Another approach is to use Voronoi's theory of perfect forms. This approach has been implemented by Sebastian Schoennenbeck [BCNS15] and, again, its output for various values of $d$ are stored in HAP. The following commands combine data from Schoennenbeck's algorithm with free resolutions for cell stabiliers to compute

$$H^1(PSL_2({\cal O}_{-6}),P_{{\cal O}_{-6}}(24)) = (\mathbb Z_2)^4 \oplus \mathbb Z_{12} \oplus \mathbb Z_{24} \oplus \mathbb Z_{9240} \oplus \mathbb Z_{55440} \oplus \mathbb Z^4\,,$$

$$H^2(PSL_2({\cal O}_{-6}),P_{{\cal O}_{-6}}(24)) = \begin{array}{l} (\mathbb Z_2)^{26} \oplus \mathbb (Z_{6})^8 \oplus \mathbb (Z_{12})^{9} \oplus \mathbb Z_{24} \oplus (\mathbb Z_{120})^2 \oplus (\mathbb Z_{840})^3\\ \oplus \mathbb Z_{2520} \oplus (\mathbb Z_{27720})^2 \oplus (\mathbb Z_{24227280})^2 \oplus (\mathbb Z_{411863760})^2\\ \oplus \mathbb Z_{2454438243748928651877425142836664498129840}\\ \oplus \mathbb Z_{14726629462493571911264550857019986988779040}\\ \oplus \mathbb Z^4\end{array}\ ,$$

$$H^3(PSL_2({\cal O}_{-6}),P_{{\cal O}_{-6}}(24)) = (\mathbb Z_2)^{23} \oplus \mathbb Z_{4} \oplus (\mathbb Z_{12})^2\ .$$

Note that the action of $SL_2({\cal O}_{-d})$ on $P_{{\cal O}_{-d}}(k)$ induces an action of $PSL_2({\cal O}_{-d})$ provided $k$ is even.

gap> R:=ResolutionPSL2QuadraticIntegers(-6,4);
Resolution of length 4 in characteristic 0 for PSL(2,O-6) . 
No contracting homotopy available. 

gap> G:=R!.group;;
gap> M:=HomogeneousPolynomials(G,24);;
gap> C:=HomToIntegralModule(R,M);;
gap> Cohomology(C,1);
[ 2, 2, 2, 2, 12, 24, 9240, 55440, 0, 0, 0, 0 ]
gap> Cohomology(C,2);
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 
  2, 6, 6, 6, 6, 6, 6, 6, 6, 12, 12, 12, 12, 12, 12, 12, 12, 12, 24, 120, 120, 
  840, 840, 840, 2520, 27720, 27720, 24227280, 24227280, 411863760, 411863760, 
  2454438243748928651877425142836664498129840, 
  14726629462493571911264550857019986988779040, 0, 0, 0, 0 ]
gap> Cohomology(C,3);
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 4, 12, 
  12 ]

We can also consider the coefficient module

$$P_{{\cal O}_{-d}}(k,\ell) = P_{{\cal O}_{-d}}(k) \otimes_{{\cal O}_{-d}} \overline{P_{{\cal O}_{-d}}(\ell)}$$

where the bar denotes a twist in the action obtained from complex conjugation. For an action of the projective linear group we must insist that $k+\ell$ is even. The following commands compute

$$H^2(PSL_2({\cal O}_{-11}),P_{{\cal O}_{-11}}(5,5)) = (\mathbb Z_2)^8 \oplus \mathbb Z_{60} \oplus (\mathbb Z_{660})^3 \oplus \mathbb Z^6\,,$$

a computation which was first made, along with many other cohomology computationsfor Bianchi groups, by Mehmet Haluk Sengun [Sen11].

gap> R:=ResolutionPSL2QuadraticIntegers(-11,3);;
gap> M:=HomogeneousPolynomials(R!.group,5,5);;
gap> C:=HomToIntegralModule(R,M);;
gap> Cohomology(C,2);
[ 2, 2, 2, 2, 2, 2, 2, 2, 60, 660, 660, 660, 0, 0, 0, 0, 0, 0 ]

The function ResolutionPSL2QuadraticIntegers(-d,n) relies on a limited data base produced by the algorithms implemented by Schoennenbeck and Rahm. The function also covers some cases covered by entering a sring "-d+I" as first variable. These cases correspond to projective special groups of module automorphisms of lattices of rank 2 over the integers of the imaginary quadratic number field $\mathbb Q(\sqrt{-d})$ with non-trivial Steinitz-class. In the case of a larger class group there are cases labelled "-d+I2",...,"-d+Ik" and the Ij together with O-d form a system of representatives of elements of the class group modulo squares and Galois action. For instance, the following commands compute

$$H_2(PSL({\cal O}_{-21+I2}),\mathbb Z) = \mathbb Z_2\oplus \mathbb Z^6\, .$$

gap> R:=ResolutionPSL2QuadraticIntegers("-21+I2",3);
Resolution of length 3 in characteristic 0 for PSL(2,O-21+I2)) . 
No contracting homotopy available. 

gap> Homology(TensorWithIntegers(R),2);
[ 2, 0, 0, 0, 0, 0, 0 ]

13.11 (Co)homology of Bianchi groups and $SL_2({\cal O}_{-d})$

The (co)homology of Bianchi groups has been studied in papers such as [SV83] [Vog85] [Ber00] [Ber06] [RF13] [Rah13b] [Rah13a] [BLR20]. Calculations in these papers can often be verified by computer. For instance, the calculation

$$H_q(PSL_2({\cal O}_{-15}),\mathbb Z) = \left\{\begin{array}{ll} \mathbb Z^2 \oplus \mathbb Z_6 & q=1,\\ \mathbb Z \oplus \mathbb Z_6 & q=2,\\ \mathbb Z_6 & q\ge 3\\ \end{array}\right.$$

obtained in [RF13] can be verified as follows, once we note that Bianchi groups have virtual cohomological dimension 2 and, if all stabilizer groups are periodic with period dividing m, then the homology has period dividing m in degree $\ge 3$.

gap> K:=ContractibleGcomplex("SL(2,O-15)");;
gap> PK:=QuotientOfContractibleGcomplex(K,Group(-One(K!.group)));;
gap> for n in [0..2] do
> for k in [1..K!.dimension(n)] do
> Print( CohomologicalPeriod(K!.stabilizer(n,k)),"  ");
> od;od;
2  2  2  2  2  2  2  2  2  2  2  2  2  2  
gap> R:=FreeGResolution(PK,5);;
gap> for n in [0..4] do
> Print("H_",n," = ", Homology(TensorWithIntegers(R),n),"\n");
> od;
H_0 = [ 0 ]
H_1 = [ 6, 0, 0 ]
H_2 = [ 6, 0 ]
H_3 = [ 6 ]
H_4 = [ 6 ]

All finite subgroups of $SL_2({\cal O}_{-d})$ are periodic. Thus the above example can be adapted from PSL to SL for any square=free $d\ge 1$. For example, the calculation

$$H^q(SL_2({\cal O}_{-2}),\mathbb Z) = \left\{\begin{array}{ll} \mathbb Z & q=1,\\ \mathbb Z_6 & q=2 \mod 4,\\ \mathbb Z_2 \oplus \mathbb Z_{12} & q= 3 \mod 4\\ \mathbb Z_2 \oplus \mathbb Z_{24} & q= 0 \mod 4 (q>0)\\ \mathbb Z_{12} & q= 1 \mod 4 (q > 1)\\ \end{array}\right.$$

obtained in [SV83] can be verified as follows.

gap> K:=ContractibleGcomplex("SL(2,O-2)");;
gap> for n in [0..2] do
> for k in [1..K!.dimension(n)] do
> Print(CohomologicalPeriod(K!.stabilizer(n,k)),"  ");
> od;od;
2  4  2  4  2  2  2  2  2  2  2  2  
gap> R:=FreeGResolution(K,11);;
gap> for n in [0..10] do
> Print("H^",n," = ", Cohomology(HomToIntegers(R),n),"\n");
> od;
H^0 = [ 0 ]
H^1 = [ 0 ]
H^2 = [ 6 ]
H^3 = [ 2, 12 ]
H^4 = [ 2, 24 ]
H^5 = [ 12 ]
H^6 = [ 6 ]
H^7 = [ 2, 12 ]
H^8 = [ 2, 24 ]
H^9 = [ 12 ]
H^10 = [ 6 ]

A quotient of a periodic group by a central subgroup of order 2 need not be periodic. For this reason the (co)homology of PSL can be a bit more tricky than SL. For example, the calculation

$$H^q(PSL_2({\cal O}_{-13}),\mathbb Z) = \left\{\begin{array}{ll} \mathbb Z^3 \oplus (\mathbb Z_2)^2 & q=1,\\ \mathbb Z^2 \oplus \mathbb Z_4 \oplus (\mathbb Z_3)^2 \oplus \mathbb Z_2 & q=2,\\ (\mathbb Z_2)^q \oplus (\mathbb Z_{3})^2 & q= 3 \mod 4\\ (\mathbb Z_2)^q & q= 0 \mod 4 (q>0)\\ (\mathbb Z_2)^q & q= 1 \mod 4 (q>1)\\ (\mathbb Z_2)^q \oplus (\mathbb Z_{3})^2 & q= 2 \mod 4 (q > 2)\\ \end{array}\right.$$

was obtained in [RF13]. The following commands verify the calculation in the first 34 degrees, but for a proof valid for all degrees one needs to analyse the computation to spot that there is a certain "periodicity of period 2" in the computations for $q\ge 3$. This analysis is done in [RF13].

gap> K:=ContractibleGcomplex("SL(2,O-13)");;
gap> PK:=QuotientOfContractibleGcomplex(K,Group(-One(K!.group)));;
gap> for n in [0..2] do
> for k in [1..PK!.dimension(n)] do
> S:=SmallGroup(IdGroup(PK!.stabilizer( n, k )));
> Print( [n,k]," is periodic ",IsPeriodic(S),"\n  ");
> od;od;
[ 0, 1 ] is periodic true
[ 0, 2 ] is periodic true
[ 0, 3 ] is periodic true
[ 0, 4 ] is periodic true
[ 0, 5 ] is periodic true
[ 0, 6 ] is periodic true
[ 0, 7 ] is periodic false
[ 0, 8 ] is periodic false
[ 1, 1 ] is periodic true
[ 1, 2 ] is periodic true
[ 1, 3 ] is periodic true
[ 1, 4 ] is periodic true
[ 1, 5 ] is periodic true
[ 1, 6 ] is periodic true
[ 1, 7 ] is periodic true
[ 1, 8 ] is periodic true
[ 1, 9 ] is periodic true
[ 1, 10 ] is periodic true
[ 1, 11 ] is periodic true
[ 1, 12 ] is periodic true
[ 1, 13 ] is periodic true
[ 2, 1 ] is periodic true
[ 2, 2 ] is periodic true
[ 2, 3 ] is periodic true
[ 2, 4 ] is periodic true
[ 2, 5 ] is periodic true
[ 2, 6 ] is periodic true
[ 2, 7 ] is periodic true
[ 2, 8 ] is periodic true
[ 2, 9 ] is periodic true
[ 2, 10 ] is periodic true
[ 2, 11 ] is periodic true

gap> R:=ResolutionPSL2QuadraticIntegers(-13,35);;
gap> for n in [0..34] do
> Print("H_",n," = ", Homology(TensorWithIntegers(R),n),"\n");
> od;
H_0 = [ 0 ]
H_1 = [ 2, 2, 0, 0, 0 ]
H_2 = [ 6, 12, 0, 0 ]
H_3 = [ 2, 6, 6 ]
H_4 = [ 2, 2, 2, 2 ]
H_5 = [ 2, 2, 2, 2, 2 ]
H_6 = [ 2, 2, 2, 2, 6, 6 ]
H_7 = [ 2, 2, 2, 2, 2, 6, 6 ]
H_8 = [ 2, 2, 2, 2, 2, 2, 2, 2 ]
H_9 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_10 = [ 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_11 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_12 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_13 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_14 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_15 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_16 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_17 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_18 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_19 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_20 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_21 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_22 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_23 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_24 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_25 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_26 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_27 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_28 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_29 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_30 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_31 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]
H_32 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_33 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_34 = [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 6, 6 ]

The Lyndon-Hochschild-Serre spectral sequence $H_p(G/N,H_q(N,A)) \implies H_{p+q}(G,A)$ for the groups $G=SL_2({\mathcal O}_{-d})$ and $N\cong C_2$ the central subgroup with $G/N\cong PSL_2({\mathcal O}_{-d})$, and the trivial module $A = \mathbb Z_{\ell}$, implies that for primes $\ell>2$ we have a natural isomorphism $H_n(PSL_2({\mathcal O}_{-d}),\mathbb Z_{\ell}) \cong H_n(SL_2({\mathcal O}_{-d}),\mathbb Z_{\ell})$. It follows that we have an isomorphism of $\ell$-primary parts $H_n(PSL_2({\mathcal O}_{-d}),\mathbb Z)_{(\ell)} \cong H_n(SL_2({\mathcal O}_{-d}),\mathbb Z)_{(\ell)}$. Since $H_n(SL_2({\mathcal O}_{-d}),\mathbb Z)_{(\ell)}$ is periodic in degrees $\ge 3$ we can recover the $3$-primary part of $H_n(PSL_2({\mathcal O}_{-13}),\mathbb Z)$ in all degrees $q\ge1$ from the following computation by ignoring all $2$-power factors in the output.

gap> R:=ResolutionSL2QuadraticIntegers(-13,13);;
gap> for n in [3..12] do
> Print("H_",n," at prime p=3 is: ", Filtered(Homology(TensorWithIntegers(R),n), m->IsInt(m/3)),"\n");
> od;
H_3 at prime p=3 is: [ 6, 24 ]
H_4 at prime p=3 is: [  ]
H_5 at prime p=3 is: [  ]
H_6 at prime p=3 is: [ 6, 12 ]
H_7 at prime p=3 is: [ 6, 24 ]
H_8 at prime p=3 is: [  ]
H_9 at prime p=3 is: [  ]
H_10 at prime p=3 is: [ 6, 12 ]
H_11 at prime p=3 is: [ 6, 24 ]
H_12 at prime p=3 is: [  ]
gap> #Ignore the 2-power factors in the output

The ring ${\mathcal O}_{-163}$ is an example of a principal ideal domain that is not a Euclidean domain. It seems that no complete calculation of $H_n(PSL_2({\mathcal O}_{-163}),\mathbb Z)$ is yet available in the literature. The following comands compute this homology in the first $31$ degrees. The computation suggests a general formula in higher degrees. All but two of the stabilizer groups for the action of $PSL_2({\mathcal O}_{-163})$ are periodic. The non-periodic group $A_4$ occurs twice in degree $0$.

gap> R:=ResolutionPSL2QuadraticIntegers(-163,32);;
gap> for n in [1..31] do
> Print("H_",n,"= ",Homology(TensorWithIntegers(R),n),"\n");
> od;
H_1= [ 0, 0, 0, 0, 0, 0, 0 ]
H_2= [ 2, 12, 0, 0, 0, 0, 0, 0 ]
H_3= [ 6 ]
H_4= [  ]
H_5= [ 2, 2, 2 ]
H_6= [ 2, 6 ]
H_7= [ 6 ]
H_8= [ 2, 2, 2, 2 ]
H_9= [ 2, 2, 2 ]
H_10= [ 2, 6 ]
H_11= [ 2, 2, 2, 2, 6 ]
H_12= [ 2, 2, 2, 2 ]
H_13= [ 2, 2, 2 ]
H_14= [ 2, 2, 2, 2, 2, 6 ]
H_15= [ 2, 2, 2, 2, 6 ]
H_16= [ 2, 2, 2, 2 ]
H_17= [ 2, 2, 2, 2, 2, 2, 2 ]
H_18= [ 2, 2, 2, 2, 2, 6 ]
H_19= [ 2, 2, 2, 2, 6 ]
H_20= [ 2, 2, 2, 2, 2, 2, 2, 2 ]
H_21= [ 2, 2, 2, 2, 2, 2, 2 ]
H_22= [ 2, 2, 2, 2, 2, 6 ]
H_23= [ 2, 2, 2, 2, 2, 2, 2, 2, 6 ]
H_24= [ 2, 2, 2, 2, 2, 2, 2, 2 ]
H_25= [ 2, 2, 2, 2, 2, 2, 2 ]
H_26= [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 6 ]
H_27= [ 2, 2, 2, 2, 2, 2, 2, 2, 6 ]
H_28= [ 2, 2, 2, 2, 2, 2, 2, 2 ]
H_29= [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 ]
H_30= [ 2, 2, 2, 2, 2, 2, 2, 2, 2, 6 ]
H_31= [ 2, 2, 2, 2, 2, 2, 2, 2, 6 ]

13.12 Some other infinite matrix groups

Analogous to the functions for Bianchi groups, HAP has functions

• ResolutionSL2QuadraticIntegers(-d,n)

• ResolutionSL2ZInvertedInteger(m,n)

• ResolutionGL2QuadraticIntegers(-d,n)

• ResolutionPGL2QuadraticIntegers(-d,n)

• ResolutionGL3QuadraticIntegers(-d,n)

• ResolutionPGL3QuadraticIntegers(-d,n)

for computing free resolutions for certain values of $SL_2({\cal O}_{-d})$, $SL_2(\mathbb Z[\frac{1}{m}])$, $GL_2({\cal O}_{-d})$ and $PGL_2({\cal O}_{-d})$. Additionally, the function

• ResolutionArithmeticGroup("string",n)

can be used to compute resolutions for groups whose data (provided by Sebastian Schoennenbeck, Alexander Rahm and Mathieu Dutour) is stored in the directory gap/pkg/Hap/lib/Perturbations/Gcomplexes .

For instance, the following commands compute

$$H^1(SL_2({\cal O}_{-6}),P_{{\cal O}_{-6}}(24)) = (\mathbb Z_2)^4 \oplus \mathbb Z_{12} \oplus \mathbb Z_{24} \oplus \mathbb Z_{9240} \oplus \mathbb Z_{55440} \oplus \mathbb Z^4\,,$$

$$H^2(SL_2({\cal O}_{-6}),P_{{\cal O}_{-6}}(24)) = \begin{array}{l} (\mathbb Z_2)^{26} \oplus \mathbb (Z_{6})^7 \oplus \mathbb (Z_{12})^{10} \oplus \mathbb Z_{24} \oplus (\mathbb Z_{120})^2 \oplus (\mathbb Z_{840})^3\\ \oplus \mathbb Z_{2520} \oplus (\mathbb Z_{27720})^2 \oplus (\mathbb Z_{24227280})^2 \oplus (\mathbb Z_{411863760})^2\\ \oplus \mathbb Z_{2454438243748928651877425142836664498129840}\\ \oplus \mathbb Z_{14726629462493571911264550857019986988779040}\\ \oplus \mathbb Z^4\end{array}\ ,$$

$$H^3(SL_2({\cal O}_{-6}),P_{{\cal O}_{-6}}(24)) = (\mathbb Z_2)^{58} \oplus (\mathbb Z_{4})^4 \oplus (\mathbb Z_{12})\ .$$

gap> R:=ResolutionSL2QuadraticIntegers(-6,4);
Resolution of length 4 in characteristic 0 for PSL(2,O-6) . 
No contracting homotopy available. 

gap> G:=R!.group;;
gap> M:=HomogeneousPolynomials(G,24);;
gap> C:=HomToIntegralModule(R,M);;
gap> Cohomology(C,1);
[ 2, 2, 2, 2, 12, 24, 9240, 55440, 0, 0, 0, 0 ]
gap> Cohomology(C,2);
gap> Cohomology(C,2);
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 
  2, 6, 6, 6, 6, 6, 6, 6, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 24, 120, 
  120, 840, 840, 840, 2520, 27720, 27720, 24227280, 24227280, 411863760, 
  411863760, 2454438243748928651877425142836664498129840, 
  14726629462493571911264550857019986988779040, 0, 0, 0, 0 ]
gap> Cohomology(C,3);
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 
  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 
  2, 2, 2, 2, 2, 2, 2, 2, 4, 4, 4, 4, 12, 12 ]

The following commands construct free resolutions up to degree 5 for the groups $SL_2(\mathbb Z[\frac{1}{2}])$, $GL_2({\cal O}_{-2})$, $GL_2({\cal O}_{2})$, $PGL_2({\cal O}_{2})$, $GL_3({\cal O}_{-2})$, $PGL_3({\cal O}_{-2})$. The final command constructs a free resolution up to degree 3 for $PSL_4(\mathbb Z)$.

gap> R1:=ResolutionSL2ZInvertedInteger(2,5);
Resolution of length 5 in characteristic 0 for SL(2,Z[1/2]) . 

gap> R2:=ResolutionGL2QuadraticIntegers(-2,5);
Resolution of length 5 in characteristic 0 for GL(2,O-2) . 
No contracting homotopy available. 

gap> R3:=ResolutionGL2QuadraticIntegers(2,5);
Resolution of length 5 in characteristic 0 for GL(2,O2) . 
No contracting homotopy available. 

gap> R4:=ResolutionPGL2QuadraticIntegers(2,5);
Resolution of length 5 in characteristic 0 for PGL(2,O2) . 
No contracting homotopy available. 

gap> R5:=ResolutionGL3QuadraticIntegers(-2,5);
Resolution of length 5 in characteristic 0 for GL(3,O-2) . 
No contracting homotopy available. 

gap> R6:=ResolutionPGL3QuadraticIntegers(-2,5);
Resolution of length 5 in characteristic 0 for PGL(3,O-2) . 
No contracting homotopy available. 

gap> R7:=ResolutionArithmeticGroup("PSL(4,Z)",3);
Resolution of length 3 in characteristic 0 for <matrix group with 655 generators> . 
No contracting homotopy available. 

13.13 Ideals and finite quotient groups

The following commands first construct the number field $\mathbb Q(\sqrt{-7})$, its ring of integers ${\cal O}_{-7}={\cal O}(\mathbb Q(\sqrt{-7}))$, and the principal ideal $I=\langle 5 + 2\sqrt{-7}\rangle \triangleleft {\cal O}(\mathbb Q(\sqrt{-7}))$ of norm ${\cal N}(I)=53$. The ring $I$ is prime since its norm is a prime number. The primality of $I$ is also demonstrated by observing that the quotient ring $R={\cal O}_{-7}/I$ is an integral domain and hence isomorphic to the unique finite field of order $53$, $R\cong \mathbb Z/53\mathbb Z$ . (In a ring of quadratic integers prime ideal is the same as maximal ideal).

The finite group $G=SL_2({\cal O}_{-7}\,/\,I)$ is then constructed and confirmed to be isomorphic to $SL_2(\mathbb Z/53\mathbb Z)$. The group $G$ is shown to admit a periodic $\mathbb ZG$-resolution of $\mathbb Z$ of period dividing $52$.

Finally the integral homology

$$H_n(G,\mathbb Z) = \left\{\begin{array}{ll} 0 & n\ne 3,7, {\rm~for~} 0\le n \le 8,\\ \mathbb Z_{2808} & n=3,7, \end{array}\right.$$

is computed.

gap> Q:=QuadraticNumberField(-7);
Q(Sqrt(-7))

gap> OQ:=RingOfIntegers(Q);
O(Q(Sqrt(-7)))

gap> I:=QuadraticIdeal(OQ,5+2*Sqrt(-7));
ideal of norm 53 in O(Q(Sqrt(-7)))

gap> R:=OQ mod I;
ring mod ideal of norm 53

gap> IsIntegralRing(R);
true

gap> gens:=GeneratorsOfGroup( SL2QuadraticIntegers(-7) );;
gap> G:=Group(gens*One(R));;G:=Image(IsomorphismPermGroup(G));;
gap> StructureDescription(G);
"SL(2,53)"

gap> IsPeriodic(G);
true
gap> CohomologicalPeriod(G);
52

gap> GroupHomology(G,1);
[  ]
gap> GroupHomology(G,2);
[  ]
gap> GroupHomology(G,3);
[ 8, 27, 13 ]
gap> GroupHomology(G,4);
[  ]
gap> GroupHomology(G,5);
[  ]
gap> GroupHomology(G,6);
[  ]
gap> GroupHomology(G,7);
[ 8, 27, 13 ]
gap> GroupHomology(G,8);
[  ]

The following commands show that the rational prime $7$ is not prime in ${\cal O}_{-5}={\cal O}(\mathbb Q(\sqrt{-5}))$. Moreover, $7$ totally splits in ${\cal O}_{-5}$ since the final command shows that only the rational primes $2$ and $5$ ramify in ${\cal O}_{-5}$.

gap> Q:=QuadraticNumberField(-5);;
gap> OQ:=RingOfIntegers(Q);;
gap> I:=QuadraticIdeal(OQ,7);;
gap> IsPrime(I);
false

gap> Factors(Discriminant(OQ));
[ -2, 2, 5 ]

For $d < 0$ the rings ${\cal O}_d={\cal O}(\mathbb Q(\sqrt{d}))$ are unique factorization domains for precisely

$$d = -1, -2, -3, -7, -11, -19, -43, -67, -163.$$

This result was conjectured by Gauss, and essentially proved by Kurt Heegner, and then later proved by Harold Stark.

The following commands construct the classic example of a prime ideal $I$ that is not principal. They then illustrate reduction modulo $I$.

gap> Q:=QuadraticNumberField(-5);;
gap> OQ:=RingOfIntegers(Q);;
gap> I:=QuadraticIdeal(OQ,[2,1+Sqrt(-5)]);
ideal of norm 2 in O(Q(Sqrt(-5)))

gap> 6 mod I;
0

13.14 Congruence subgroups for ideals

Given a ring of integers ${\cal O}$ and ideal $I \triangleleft {\cal O}$ there is a canonical homomorphism $\pi_I\colon SL_2({\cal O}) \rightarrow SL_2({\cal O}/I)$. A subgroup $\Gamma \le SL_2({\cal O})$ is said to be a congruence subgroup if it contains $\ker \pi_I$. Thus congruence subgroups are of finite index. Generalizing the definition in 13.1 above, we define the principal congruence subgroup $\Gamma_1(I)=\ker \pi_I$, and the congruence subgroup $\Gamma_0(I)$ consisting of preimages of the upper triangular matrices in $SL_2({\cal O}/I)$.

The following commands construct $\Gamma=\Gamma_0(I)$ for the ideal $I\triangleleft {\cal O}\mathbb Q(\sqrt{-5})$ generated by $12$ and $36\sqrt{-5}$. The group $\Gamma$ has index $385$ in $SL_2({\cal O}\mathbb Q(\sqrt{-5}))$. The final command displays a tree in a Cayley graph for $SL_2({\cal O}\mathbb Q(\sqrt{-5}))$ whose nodes represent a transversal for $\Gamma$.

gap> Q:=QuadraticNumberField(-5);;
gap> OQ:=RingOfIntegers(Q);;
gap> I:=QuadraticIdeal(OQ,[36*Sqrt(-5), 12]);;
gap> G:=HAP_CongruenceSubgroupGamma0(I);
CongruenceSubgroupGamma0(ideal of norm 144 in O(Q(Sqrt(-5)))) 

gap> IndexInSL2O(G);
385
 
gap> HAP_SL2TreeDisplay(G);

The next commands first construct the congruence subgroup $\Gamma_0(I)$ of index $144$ in $SL_2({\cal O}\mathbb Q(\sqrt{-2}))$ for the ideal $I$ in ${\cal O}\mathbb Q(\sqrt{-2})$ generated by $4+5\sqrt{-2}$. The commands then compute

$$H_1(\Gamma_0(I),\mathbb Z) = \mathbb Z_3 \oplus \mathbb Z_6 \oplus \mathbb Z_{30} \oplus \mathbb Z^8\, ,$$

$$H_2(\Gamma_0(I), \mathbb Z) = (\mathbb Z_2)^9 \oplus \mathbb Z^7\, ,$$

$$H_3(\Gamma_0(I), \mathbb Z) = (\mathbb Z_2)^9 \, .$$

gap> Q:=QuadraticNumberField(-2);;
gap> OQ:=RingOfIntegers(Q);;
gap> I:=QuadraticIdeal(OQ,4+5*Sqrt(-2));;
gap> G:=HAP_CongruenceSubgroupGamma0(I);
CongruenceSubgroupGamma0(ideal of norm 66 in O(Q(Sqrt(-2)))) 

gap> IndexInSL2O(G);
144

gap> R:=ResolutionSL2QuadraticIntegers(-2,4,true);;
gap> S:=ResolutionFiniteSubgroup(R,G);;

gap> Homology(TensorWithIntegers(S),1);
[ 3, 6, 30, 0, 0, 0, 0, 0, 0, 0, 0 ]
gap> Homology(TensorWithIntegers(S),2);
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0 ]
gap> Homology(TensorWithIntegers(S),3);
[ 2, 2, 2, 2, 2, 2, 2, 2, 2 ]

13.15 First homology

The isomorphism $H_1(G,\mathbb Z) \cong G_{ab}$ allows for the computation of first integral homology using computational methods for finitely presented groups. Such methods underly the following computation of

$$H_1( \Gamma_0(I),\mathbb Z) \cong \mathbb Z_2 \oplus \cdots \oplus \mathbb Z_{4078793513671}$$

where $I$ is the prime ideal in the Gaussian integers generated by $41+56\sqrt{-1}$.

gap> Q:=QuadraticNumberField(-1);;
gap> OQ:=RingOfIntegers(Q);;
gap> I:=QuadraticIdeal(OQ,41+56*Sqrt(-1));
ideal of norm 4817 in O(GaussianRationals)
gap> G:=HAP_CongruenceSubgroupGamma0(I);;
gap> AbelianInvariants(G);
[ 2, 2, 4, 5, 7, 16, 29, 43, 157, 179, 1877, 7741, 22037, 292306033, 
  4078793513671 ]

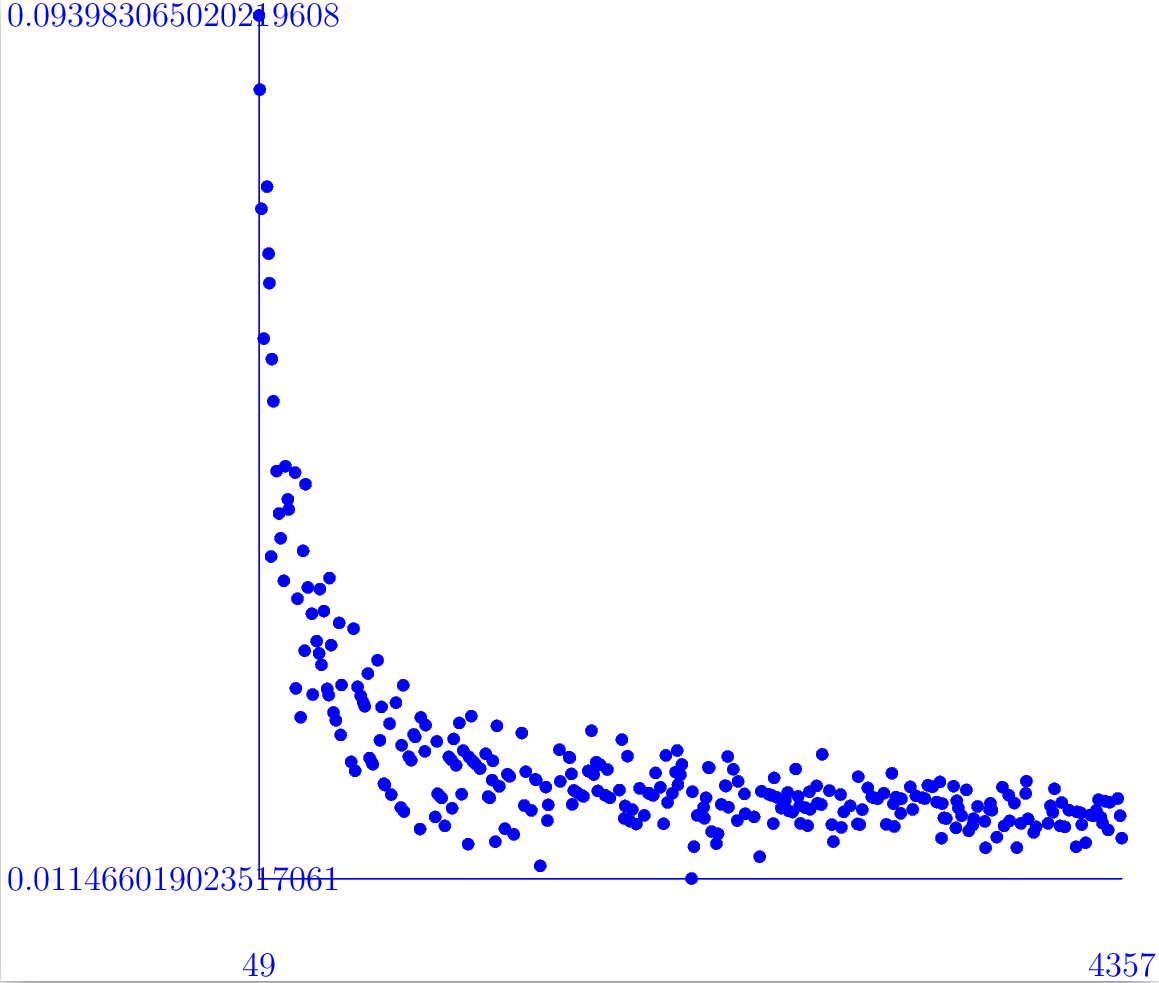
We write $G^{ab}_{tors}$ to denote the maximal finite summand of the first homology group of $G$ and refer to this as the torsion subgroup. Nicholas Bergeron and Akshay Venkatesh [Ber16] have conjectured relationships between the torsion in congruence subgroups $\Gamma$ and the volume of their quotient manifold ${\frak h}^3/\Gamma$. For instance, for the Gaussian integers they conjecture

$$\frac{\log |\Gamma_0(I)_{tors}^{ab}|}{{\rm Norm}(I)} \rightarrow \frac{\lambda}{18\pi},\ \lambda =L(2,\chi_{\mathbb Q(\sqrt{-1})}) = 1 -\frac{1}{9} + \frac{1}{25} - \frac{1}{49} + \cdots$$

as the norm of the prime ideal $I$ tends to $\infty$. The following approximates $\lambda/18\pi = 0.0161957$ and $\frac{\log |\Gamma_0(I)_{tors}^{ab}|}{{\rm Norm}(I)} = 0.0210325$ for the above example.

gap> Q:=QuadraticNumberField(-1);;
gap> Lfunction(Q,2)/(18*3.142);
0.0161957

Loge10:=0.434294481903;; #Log_10(e)
gap> 1.0*Log(Product(AbelianInvariants(G)),10)/(Loge*Norm(I));
0.0210325

The link with volume is given by the Humbert volume formula

$${\rm Vol} ( {\frak h}^3 / PSL_2( {\cal O}_{d} ) ) = \frac{|D|^{3/2}}{24} \zeta_{ \mathbb Q( \sqrt{d} ) }(2)/\zeta_{\mathbb Q}(2)$$

valid for square-free $d<0$, where $D$ is the discriminant of $\mathbb Q(\sqrt{d})$. The volume of a finite index subgroup $\Gamma$ is obtained by multiplying the right-hand side by the index $|PSL_2({\cal O}_d)\,:\, \Gamma|$.

The following commands produce a graph of $\frac{\log |\Gamma_0(I)_{tors}^{ab}|}{{\rm Norm}(I)}$ against ${\rm Norm}(I)$ for prime ideals $I$ of norm $49 \le {\rm Norm}(I) \le 4357$ (where one ideal for each norm is taken).

gap> Q:=QuadraticNumberField(-1);;
gap> OQ:=RingOfIntegers(Q);;
gap> N:=QuadraticIntegersByNorm(OQ,20000);;

gap> #########################################
gap> fn:=function(x);
gap> if IsRat(x) then return x; fi;
gap> return x!.rational+x!.irrational*Sqrt(-1);
gap> end;
gap> #########################################

gap> NN:=List(N,fn);
gap> P:=Filtered(NN,x->IsPrime(QuadraticIdeal(OQ,x)));
gap> PP:=Classify(P,x->Norm(Q,x));
gap> PP:=List(PP,x->x[1]);;
gap> PP:=Filtered(PP,x->not x=0);

gap> Loge:=0.434294481903;; ###Log_10(e)
gap> #########################################
gap> ffn:=function(x)
gap> local I, G, A, S, F;
gap> I:=QuadraticIdeal(OQ,x);
gap> G:=HAP_CongruenceSubgroupGamma0(I);;
gap> A:=AbelianInvariants(G);
gap> A:=Filtered(A,x->not x=0);
gap> return [Norm(Q,x),1.0*Log(Product(Filtered(AbelianInvariants(G),i->not i=0)),10)/(Loge*Norm(I))];
gap> end;
gap> #########################################

gap> S:=List(PP{[9..267]},ffn);
gap> ScatterPlot(S);

generated by GAPDoc2HTML