About HAP: Knots and Quandles

Knots and Quandles
Sub-package by Cédric FRAGNAUD and Graham ELLIS
A quandle (Q, ▹) is a non-empty set Q equipped with a binary operation ▹ : Q × Q → Q satisfying the following axioms:

1/ ∀∃∈For all a ∈ Q, a ▹ a = a.
2/ ∀ a, b ∈ Q, ∃! c ∈ Q such that a = c ▹ b.
3/ ∀ a, b, c ∈ Q, (a ▹ b) ▹ c = (a ▹ c) ▹ (b ▹ c).

One can check that for any group G and n ∈ ℤ, the magma (G, ▹) forms a quandle with the operation x ▹ y = y-nxyn , ∀ x, y ∈ G. Such a quandle is called the n-Fold Conjugation Quandle.

A quandle Q is said to be connected if the inner automorphism group Inn Q acts transitively on Q. In other words, Q is connected if and only if for each pair a, b in Q there are a1, a2, . . . , an in Q such that a ▹ a1 ▹· · · ▹ an = b.

A quandle Q is said to be latin if ∀ a, b ∈ Q, ∃ c ∈ Q such that a = b ▹ c.
gap> Q:=Quandle(5,21);
<magma with 5 generators>
gap> Display(MultiplicationTable(Q));
[ [  1,  3,  4,  5,  2 ],
  [  3,  2,  5,  1,  4 ],
  [  4,  5,  3,  2,  1 ],
  [  5,  1,  2,  4,  3 ],
  [  2,  4,  1,  3,  5 ] ]
gap> IsConnectedQuandle(Q);
true
gap> IsLatin(Q);
true
Let Q be a set, e an element in Q, G a permutation group, and stigma an element in G.
Then (Q,G,e,stigma) describes a Quandle Envelope if :
  • G is a transitive group on Q.
  • stigma ∈ Z(Ge), the center of the stabilizer of e.
  • ⟨stigmaG⟩ = G (that is, the smallest normal subgroup of G containing stigma is all of G).

From a Quandle Envelope (Q,G,e,stigma), we can construct a Quandle (Q, ▹):

        for all x,y in Q,        x ▹ y=(ŷ(stigma))(x)        , where ŷ ∈ G satisfies ŷ(e)=y.

Such a quandle is connected. This property is used to construct all the connected quandles of size n.
gap> Q:=[1..9];; e:=2;; G:=TransitiveGroup(9,15);; st:=(1,8,7,4,9,5,3,6);;
gap> IsQuandleEnvelope(Q,G,e,st); QE:=QuandleQuandleEnvelope(Q,G,e,st);
true
<magma with 9 generators>
gap> IsQuandle(QE); IsConnectedQuandle(QE);
true
true
gap> ConnectedQuandles(20); time;
[ <magma with 20 generators>, <magma with 20 generators>, <magma with 20 generators>,
  <magma with 20 generators>, <magma with 20 generators>, <magma with 20 generators>,
  <magma with 20 generators>, <magma with 20 generators>, <magma with 20 generators>,
  <magma with 20 generators> ]
3364296
Let's denote Rx the mapping defined by Rx : Q→Q, y ↦y▹x.
We define the right multiplication group G of a quandle Q by G=〈Rx, x ∈ Q〉.
We also define the automorphism group Aut(Q)={f:Q→Q}.
It can be proven that Rx is a subgroup of Aut(Q).
gap> Q:=ConnectedQuandle(8,2);; q:=Random(Q);
m6
gap> A:=AutomorphismGroupQuandle(Q);; a:=Random(A);;
gap> q^a;
m4
gap> R:=RightMultiplicationGroupOfQuandle(Q);; r:=Random(R);;
gap> q^r;
m3
A knot is an embedding of the circle S1 in ℝ3.

To study these structures, we use knot diagrams, which are projections of these knots into ℝ2, defined, for instance, by f : ℝ3 → ℝ2; (x,y,z) → (x,y)  subject to the constraint that the preimage of any (x, y) ∈ ℝ2 contains at most two points.

Crossing points occur when the preimage of a point in ℝ2 contains more than one point.

At these crossing points, we denote the point in the preimage that is nearer to the ℝ2 plane as the under-crossing point and the point farther away as the over-crossing point. An arc is a line that connects two crossing points in the knot diagram, with a line break occurring when an undercrossing point is mapped to the arc.

We may give a knot diagram an orientation, i.e. a direction of travelling around the knot. This allows us to categorize crossings as either positive or negative:
A positive and neative crossing

There exists different ways to describe a knot diagram: Planar Diagram, Gauss Code, Dowker Notation, Conway Notation.
An other way to describe a knot is to use quandles. From a knot K, we can construct the knot quandle Q(K), whose generators are the arcs of K, and relations are associated to the crossings:

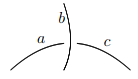
Relators knot quandles
This figure gives us "a ▹ b = c" at a negative crossing, and "a ▹-1 b = c" (or "c ▹ b = a") at a positive one.
gap> K:=PureCubicalKnot(3,1);;
gap> G:=GaussCodeOfPureCubicalKnot(K);;
gap> P:=PresentationKnotQuandle(G);
rec( generators := [ 1 .. 3 ], relators := [ [ [ 3, 2 ], 1 ], [ [ 1, 3 ], 2 ], [ [ 2, 1 ], 3 ] ] )
From this example, we see that the generators of the Trefoil Knot Quandle are the arcs 1, 2 and 3; these generators satisfy the relations above.

Nb: [[a1 ,a2 ],a3 ] means a1 ▹ a2 = a3, no matter if we consider a positive or negative crossing.
We can also easily go from a Planar Diagram representation of a knot to a its Gauss Code (with orientations of crossings).
gap> PD:=PlanarDiagramKnot(3,1);
[ [ 1, 4, 2, 5 ], [ 3, 6, 4, 1 ], [ 5, 2, 6, 3 ] ]
gap> G:=PD2GC(PD);
[ [ [ -1, 3, -2, 1, -3, 2 ] ], [ -1, -1, -1 ] ]
Using quandles, we can construct an knot invariant: a list made of the number of Homomorphisms beetween the knot (in the form of a record) and a connected quandle.
gap> K:=PresentationKnotQuandleKnot(8,2);
rec( generators := [ 1 .. 8 ], relators := [ [ [ 8, 2 ], 1 ], [ [ 2, 5 ], 1 ], [ [ 2, 6 ], 3 ], [ [ 3, 7 ], 4 ], [ [ 4, 8 ], 5 ],
[ [ 6, 1 ], 5 ], [ [ 6, 3 ], 7 ], [ [ 7, 4 ], 8 ] ] )
gap> Q:=ConnectedQuandle(9,2);;
gap> NumberHommorphism(Q,K); time;
9
216228
gap> Invariant(K,9); time;
[ 1, 3, 4, 5, 5, 5, 6, 6, 7, 7, 7, 7, 7, 64, 64, 8, 9, 9, 9, 9, 81, 9, 9, 9 ]
1327036
Previous Page
 Contents
 Next page