AboutHap

Previous

About HAP: Explicit cocycles

next

Given a ZG-resolution R and a ZG-module A, one defines an n-cocycle to be a ZG-homomorphism f:R_n→ A for which the composite homomorphism fd_n+1:R_n+1→A is zero. If R happens to be the standard bar resolution (i.e. the cellular chain complex of the nerve of the group G considered as a one object category) then the free ZG-generators of R_n are indexed by n-tuples (g₁ | g₂ | ... | g_n) of elements g_i in G. In this case we say that the n-cocycle is a standard n-cocycle and we think of it as a set-theoretic function

f : G × G × ... × G → A

satisfying a certain algebraic cocycle condition.

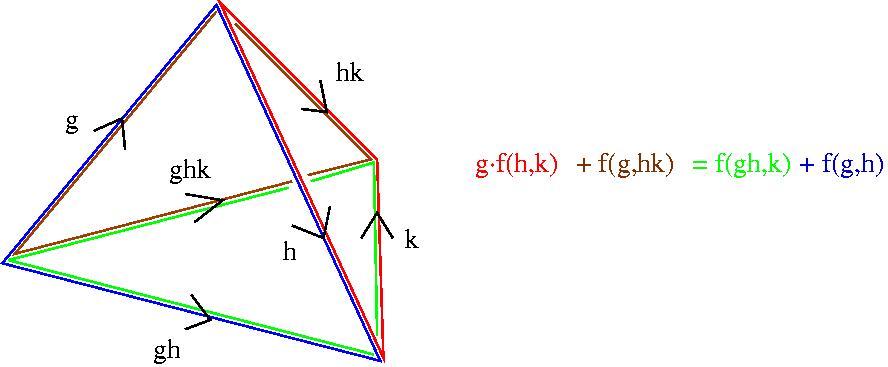
Bearing in mind that a standard n-cocycle really just assigns an element f(g₁, ... ,g_n) of A to an n-simplex in the nerve of G, the cocycle condition is a very natural one which states that "f must vanish on the boundary of a certain (n+1)-simplex". For n=2 the condition is that a 2-cocycle f(g₁,g₂) must satisfy g.f(h,k) + f(g,hk) = f(gh,k) + f(g,h) for all g,h,k in G. This equation is explained by the following picture.

The definition of a cocycle clearly depends on the choice of ZG-resolution R. However, the cohomology group Hⁿ(G,A), which is a group of equivalence classes of n-cocycles, is independent of the choice of R.

There are some occasions when one needs explicit examples of standard cocycles. For instance:

Let G be a finite group and K a field of characteristic 0. The group algebra K(G) and the algebra F(G) of functions đ_g:G→K, h→đ_g,h are both Hopf algebras. The tensor product F(G) (×) K(G) also admits a Hopf algebra structure known as the quantum double D(G). A twisted quantum double D^f(G) was introduced in [R. Dijkraaf, V. Pasquier & P. Roche, "Quasi-Hopf algebras, group cohomology and orbifold models", Nuclear Phys. B Proc. Suppl. 18B (1991) 60-72]. The twisted double is a quasi-Hopf algebra depending on a 3-cocycle f:G×G×G→K. The multiplication is given by (đ_g (×) x)(đ_h (×) x) = đ_gx,xhß_g(x,y)(đ_g (×) xy) where ß_a is defined by ß_a(h,g) = f(a,h,g) f(h,h^-1ah,g)^-1 f(h,g,(hg)^-1ahg) . Although the algebraic structure of D^f(G) depends very much on the particular 3-cocycle f, representation theoretic properties of D^f(G) depend only on the cohomology class of f.
An explicit 2-cocycle f:G×G→A is needed to construct the multiplication (a,g)(a',g') = (a + g·a' + f(g,g'), gg') in the extension a group G by a ZG-module A determined by the cohomology class of f in H²(G,A).
In work on coding theory and Hadamard matrices a number of papers have investigated square matrices (a_ij) whose entries a_ij=f(g_i,g_j) are the values of a 2-cocycle f:G×G → Z₂ where G is a finite group acting trivially on Z₂. See for instance [K.J. Horadam, "An introduction to cocyclic generalised Hadamard matrices", Discrete Applied Math, 102 (2000) 115-130].

Given a ZG-resolution R (with contracting homotopy) and a ZG-module A one can use HAP commands to compute explicit standard n-cocycles f:Gⁿ → A. With the twisted quantum double in mind, we illustrate the computation for n=3, G=S₃, and A=U(1) the group of complex numbers of modulus 1 with trivial G-action.

We first compute a ZG-resolution R. The Universal Coefficient Theorem gives an isomorphism H³(G,U(1)) = Hom_Z(H₃(G,Z), U(1)), The multiplicative group U(1) can thus be viewed as Z_m where m is a multiple of the exponent of H₃(G,Z).

gap> G:=SymmetricGroup(3);;
gap> R:=ResolutionFiniteGroup(G,4);;
gap> TR:=TensorWithIntegers(R);;
gap> Homology(TR,3);
[ 6 ]

gap> R.dimension(3);
4
gap> R.dimension(4);
5

We thus replace the very infinite group U(1) by the finite cyclic group Z₆. Since the resolution R has 4 generators in degree 3, a homomorphism f:R₃→U(1) can be represented by a list f=[f₁, f₂, f₃, f₄] with f_i is the image in Z₆ of the ith generator. The cocycle condition on f can be expressed as a matrix equation

Mf = 0 modulo 6

where the matrix M is got from the following command.

gap> M:=CocycleCondition(R,3);;

A particular cocycle f=[f₁, f₂, f₃, f₄] can be got by choosing a solution to the equation Mf=0.

gap> SolutionsMod2:=NullspaceModQ(TransposedMat(M),2);
[ [ 0, 0, 0, 0 ], [ 0, 0, 1, 1 ], [ 1, 1, 0, 0 ], [ 1, 1, 1, 1 ] ]

gap> SolutionsMod3:=NullspaceModQ(TransposedMat(M),3);
[ [ 0, 0, 0, 0 ], [ 0, 0, 0, 1 ], [ 0, 0, 0, 2 ], [ 0, 0, 1, 0 ],
[ 0, 0, 1, 1 ], [ 0, 0, 1, 2 ], [ 0, 0, 2, 0 ], [ 0, 0, 2, 1 ],
[ 0, 0, 2, 2 ] ]

A non-standard 3-cocycle f can be converted to a standard one using the command StandardCocycle(R,f,n,q) . This command inputs R, integers n and q, and an n-cocycle f for the resolution R. It returns a standard cocycle Gⁿ → Z_q.

gap> f:=3*SolutionsMod2[3] - SolutionsMod3[5]; #An example solution to Mf=0 mod 6.
[ 3, 3, -1, -1 ]

gap> Standard_f:=StandardCocycle(R,f,3,6);;

gap> g:=Random(G); h:=Random(G); k:=Random(G);
(1,2)
(1,3,2)
(1,3)

gap> Standard_f(g,h,k);
3

A function f: G×G×G → A is a standard 3-cocycle if and only if

g·f(h,k,l) - f(gh,k,l) + f(g,hk,l) - f(g,h,kl) + f(g,h,k) = 0

for all g,h,k,l in G. In the above example the group G=S₃ acts trivially on A=Z₆. The following commands show that the standard 3-cocycle produced in the example really does satisfy this 3-cocycle condition.

gap> sf:=Standard_f;;

gap> Test:=function(g,h,k,l);
> return sf(h,k,l) - sf(g*h,k,l) + sf(g,h*k,l) - sf(g,h,k*l) + sf(g,h,k);
> end;
function( g, h, k, l ) ... end

gap> for g in G do for h in G do for k in G do for l in G do
> Print(Test(g,h,k,l),",");
> od;od;od;od;
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,6,6,0,0,6,
0,0,0,0,0,6,6,6,0,6,0,12,12,6,12,6,0,12,6,0,6,6,0,0,0,0,0,0,0,12,12,6,6,6,0,
6,6,0,6,6,0,0,-6,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,0,0,0,0,0,0,6,0,0,6,6,0,6,6,
0,6,0,0,6,6,6,0,0,0,0,0,0,0,-6,0,0,-6,0,-6,0,0,0,0,0,0,0,0,6,6,0,6,0,0,6,0,0,
0,0,0,6,6,6,0,0,0,6,6,6,0,0,0,0,-6,0,6,6,0,0,0,0,0,0,0,12,6,6,0,6,0,0,0,0,12,
6,0,0,0,0,0,0,0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,6,0,0,6,0,0,0,0,0,6,6,
6,0,0,0,6,12,6,6,0,0,0,-6,0,0,6,0,0,0,0,0,0,0,12,12,6,6,6,0,0,0,0,6,6,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,6,0,6,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,
6,6,0,6,6,0,12,12,6,12,12,0,0,0,0,0,0,0,6,6,0,0,0,0,6,6,6,12,12,0,-6,-6,0,0,
0,0,6,6,0,0,6,0,0,6,0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,
0,6,0,0,6,0,0,0,0,0,0,0,0,0,0,0,6,6,0,6,0,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,6,6,0,6,6,0,6,0,0,6,6,6,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,0,0,0,0,0,0,0,6,6,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0,0,-6,0,6,0,6,0,6,0,0,0,0,0,0,0,12,12,6,12,12,0,6,6,0,6,6,0,
0,0,0,0,0,0,12,12,6,12,12,0,6,6,0,6,6,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,
0,0,0,0,0,0,6,0,0,6,6,0,6,6,0,6,0,0,6,6,6,0,0,0,-6,0,0,0,-6,0,0,-6,0,-6,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,6,6,0,0,0,0,0,0,0,6,6,0,0,0,
0,0,0,0,6,6,0,-6,0,0,-6,0,0,12,6,0,-6,-6,0,0,0,0,6,6,0,0,6,0,0,6,0,6,6,0,0,0,
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,-6,0,0,0,0,0,0,0,0,0,0,6,6,6,6,6,0,6,12,0,6,0,0,6,0,0,0,6,0,0,0,0,0,0,
0,6,12,0,0,0,0,0,0,0,6,6,0,-6,-6,0,0,0,0,0,0,0,0,6,0,0,6,0,6,6,0,0,0,0,0,0,0,
6,0,0,0,6,0,0,6,0,6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,6,
0,0,0,0,0,0,0,0,6,0,0,0,0,0,0,0,6,6,0,6,6,0,6,6,6,12,12,0,0,0,0,0,0,0,6,6,0,
6,6,0,6,6,6,12,12,0,0,0,0,0,0,0,6,6,0,0,6,0,0,6,0,6,6,

Previous Page

Contents